题目内容

3．已知a=20.3，b=log0.23，c=log32，则a，b，c的大小关系是（　　）
A．a＜b＜cB．c＜b＜aC．b＜a＜cD．b＜c＜a

分析 利用对数函数、指数函数的单调性求解．

解答 解：∵a=20.3＞20=1，
b=log0.23＜log0.21=0，
0=log31＜c=log32＜log33=1，
∴a，b，c的大小关系是b＜c＜a．
故选：D．

点评 本题考查三个数的大小的比较，是基础题，解题时要认真审题，注意利用对数函数、指数函数的单调性的合理运用．

练习册系列答案
相关题目
13．函数y=sin2x+2cosx在R上的值域是[-2，2]．
14．已知cosθ＞0，tan（θ+$\frac{π}{4}$）=$\frac{1}{3}$，则θ在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
11．在长方体ABCD-A1B1C1D1中，AB=BC=$\sqrt{3}$，AA1=1，则异面直线AD与BC1所成角为（　　）
A．30°B．45°C．60°D．90°
18．若直线（a+1）x+ay=0与直线ax+2y=1垂直，则实数a=0或-3．
8．已知偶函数f（x）在[0，+∞）上是增函数，且f（1）=0，则满足f（log${\;}_{\frac{1}{2}}$x）＞0的x的取值范围是（　　）
A．（0，+∞）B．（0，$\frac{1}{2}$）∪（2，+∞）C．（0，$\frac{1}{2}$）D．（0，$\frac{1}{2}$）∪（1，2）
15．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，x≤1}\\{{2}^{-x}，x＞1}\end{array}\right.$，则f（f（2））=（　　）
A．$\frac{1}{16}$B．16C．$\frac{1}{4}$D．4
12．已知△ABC是钝角三角形，若AC=1，BC=2，且△ABC的面积为$\frac{{\sqrt{3}}}{2}$，则AB=（　　）
A．$\sqrt{3}$B．$\sqrt{7}$C．$2\sqrt{2}$D．3
13．图中的三个直角三角形是一个体积为20cm3几何体的三视图，则h=（　　）
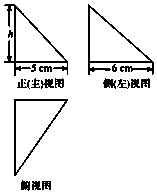
A．4B．5C．6D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网