题目内容
以双曲线y2-x2=2的一个焦点为圆心，离心率为半径的圆的方程是（ ）
| A、x2+（y±2）2=2 |
| B、（x±2）2+y2=2 |
| C、x2+（y±2）2=4 |
| D、（x±2）2+y2=4 |
考点：双曲线的简单性质
专题：直线与圆,圆锥曲线的定义、性质与方程
分析：首先根据已知条件求出双曲线的离心率和焦点坐标，进一步求出圆的方程．
解答：
解：双曲线y2-x2=2的焦点坐标为（0，2）和（0，-2），
离心率为
．
则：以焦点为圆心，离心率为半径的圆的方程为：x2+（y±2）2=2
故选：A
离心率为
| 2 |
则：以焦点为圆心，离心率为半径的圆的方程为：x2+（y±2）2=2
故选：A
点评：本题考查的知识要点：等轴双曲线的离心率和焦点坐标的应用．属于基础题型．
练习册系列答案
名校课堂系列答案
相关题目
设x，y满足约束条件
则z=x-2y的最小值为（ ）
|
| A、-10 | B、-6 | C、-1 | D、0 |
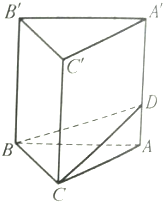已知正三棱柱的底面边长是4厘米，过BC的一个平面与底面成30°的二面角，交侧棱AA′于D，求AD的长和截面△BCD的面积．已知各顶点都在一个球面上的正方体的体积为8，则这个球的表面积是（ ）
| A、8π | B、12π |
| C、16π | D、20π |