题目内容
已知关于x的函数f(x)=x2+2mx+m
(1)若函数f(x)没有零点,求实数m的取值范围;
(2)当m=2时,求函数g(x)=
在区间[1,2]上的最大值,并求出相应的x的值.
(1)若函数f(x)没有零点,求实数m的取值范围;
(2)当m=2时,求函数g(x)=
| f(x) |
| x |
考点:利用导数求闭区间上函数的最值,函数的零点
专题:计算题,函数的性质及应用
分析:(1)由f(x)=x2+2mx+m没有零点可得△=(2m)2-4m<0;从而解得;
(2)化简g(x)=
=x+
+4;从而利用对勾函数的性质求最大值即最大值点.
(2)化简g(x)=
| f(x) |
| x |
| 2 |
| x |
解答:
解:(1)∵f(x)=x2+2mx+m没有零点,
∴△=(2m)2-4m<0;
故0<m<1;
(2)当m=2时,f(x)=x2+4x+2;
g(x)=
=x+
+4;
由对勾函数的性质可得,
g(x)=x+
+4在[1,
]上单调递减,在[
,2]上单调递增;
且g(1)=1+2+4=7;g(2)=2+1+4=7;
故当x=1或x=2时,
函数g(x)=
在区间[1,2]上取得最大值7.
∴△=(2m)2-4m<0;
故0<m<1;
(2)当m=2时,f(x)=x2+4x+2;
g(x)=
| f(x) |
| x |
| 2 |
| x |
由对勾函数的性质可得,
g(x)=x+
| 2 |
| x |
| 2 |
| 2 |
且g(1)=1+2+4=7;g(2)=2+1+4=7;
故当x=1或x=2时,
函数g(x)=
| f(x) |
| x |
点评:本题考查了二次函数的性质与对勾函数的性质应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
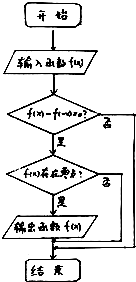 执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )
执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )