题目内容
设函数f(x)=lnx-mx(m>0).
(Ⅰ)求函数f(x)的单调性;
(Ⅱ)判断函数f(x)在区间[1,e]上的零点个数.
(Ⅰ)求函数f(x)的单调性;
(Ⅱ)判断函数f(x)在区间[1,e]上的零点个数.
考点:根的存在性及根的个数判断,利用导数研究函数的单调性
专题:函数的性质及应用,导数的概念及应用
分析:(1)先研究函数的定义域,然后根据导数大于零求增区间,导数小于零求减区间,注意分类讨论;
(2)结合(1)中函数的单调性,研究函数在该区间上的极值,最值以及端点值的符号,最终确定函数在该区间上零点的个数.
(2)结合(1)中函数的单调性,研究函数在该区间上的极值,最值以及端点值的符号,最终确定函数在该区间上零点的个数.
解答:
解:(Ⅰ)由题得f′(x)=
-m=
(x>0,m>0),
当0<x<
时,f'(x)>0;当x>
时,f'(x)<0,
所以函数f(x)的单调递增区间是(0,
),单调递减区间是(
,+∞),
(Ⅱ)由(Ⅰ)知函数f(x)在(0,
)上单调递增,在(
,+∞)上单调递减,
所以函数f(x)在区间[1,e]上最多有2个零点,
而且f(x)max=f(
)=ln
-1,f(1)=-m<0;
(ⅰ)若函数f(x)在区间[1,e]上有2个零点,
则
,此不等式组无解,
所以不存在m>0,使函数f(x)在区间[1,e]上有2个零点;
(ⅱ) 若函数f(x)在区间[1,e]上仅有1个零点,
则
,解得0<m≤
,
所以当0<m≤
时,函数f(x)在区间[1,e]上仅有1个零点,
(ⅲ) 若函数f(x)在区间[1,e]上无零点,
结合(ⅱ)知m>
,即0<
<e,
则
,解得m>
,
所以当m>
时,函数f(x)在区间[1,e]上无零点.
综上所述,当0<m≤
时,函数f(x)在区间[1,e]上有1个零点,
当m>
时,函数f(x)在区间[1,e]上无零点.
| 1 |
| x |
-m(x-
| ||
| x |
当0<x<
| 1 |
| m |
| 1 |
| m |
所以函数f(x)的单调递增区间是(0,
| 1 |
| m |
| 1 |
| m |
(Ⅱ)由(Ⅰ)知函数f(x)在(0,
| 1 |
| m |
| 1 |
| m |
所以函数f(x)在区间[1,e]上最多有2个零点,
而且f(x)max=f(
| 1 |
| m |
| 1 |
| m |
(ⅰ)若函数f(x)在区间[1,e]上有2个零点,
则
|
所以不存在m>0,使函数f(x)在区间[1,e]上有2个零点;
(ⅱ) 若函数f(x)在区间[1,e]上仅有1个零点,
则
|
| 1 |
| e |
所以当0<m≤
| 1 |
| e |
(ⅲ) 若函数f(x)在区间[1,e]上无零点,
结合(ⅱ)知m>
| 1 |
| e |
| 1 |
| m |
则
|
| 1 |
| e |
所以当m>
| 1 |
| e |
综上所述,当0<m≤
| 1 |
| e |
当m>
| 1 |
| e |
点评:本题考查了函数的单调区间的求法,以及利用导数研究函数的极值、最值和端点值,最终确定函数在区间上的零点个数的方法.要注意结合图象解决问题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知点P是抛物线y2=4x上一点,设点P到此抛物线的准线的距离为d1,到直线x+2y-12=0的距离为d2,则d1+d2的最小值是( )
| A、5 | ||||
| B、4 | ||||
C、
| ||||
D、
|
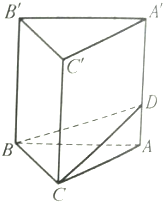 已知正三棱柱的底面边长是4厘米,过BC的一个平面与底面成30°的二面角,交侧棱AA′于D,求AD的长和截面△BCD的面积.
已知正三棱柱的底面边长是4厘米,过BC的一个平面与底面成30°的二面角,交侧棱AA′于D,求AD的长和截面△BCD的面积.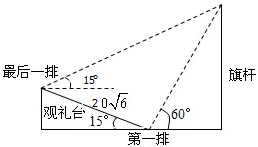 2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一垂直于地面的平面上,在该列的第一排B处和最后一排A处测得旗杆顶端的仰角为15°,且第一排和最后一排的距离为20
2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一垂直于地面的平面上,在该列的第一排B处和最后一排A处测得旗杆顶端的仰角为15°,且第一排和最后一排的距离为20