题目内容
已知A(-2,4),B(3,-1),C(-3,-4),设
=
,
=
,
=
,
=3
,
=-2
,
求:(1)2
+
-3
;
(2)满足
=m
+n
的实数m,n;
(3)M,N的坐标及向量
的坐标.
| AB |
| a |
| BC |
| b |
| CA |
| c |
| CM |
| c |
| CN |
| b |
求:(1)2
| a |
| b |
| c |
(2)满足
| a |
| b |
| c |
(3)M,N的坐标及向量
| MN |
考点:向量加减混合运算及其几何意义,平面向量的坐标运算
专题:平面向量及应用
分析:(1)根据题意,求出向量
、
、
,计算2
+
-3
即可;
(2)由向量相等,其坐标对应相等,列出方程组,求出m、n的值;
(3)设出M(x1,y1),N(x2,y2),根据向量相等,求出M、N的坐标,再求向量
的坐标表示.
| a |
| b |
| c |
| a |
| b |
| c |
(2)由向量相等,其坐标对应相等,列出方程组,求出m、n的值;
(3)设出M(x1,y1),N(x2,y2),根据向量相等,求出M、N的坐标,再求向量
| MN |
解答:
解:(1)∵A(-2,4),B(3,-1),C(-3,-4),
=
,
=
,
=
,
∴
=(5,-5),
=(-6,-3),
=(1,8),
∴2
+
-3
=2(5,-5)+(-6,-3)-3(1,8)=(10-6-3,-10-3-24)=(1,-37);
(2)∵
=m
+n
,
∴(5,-5)=m(-6,-3)+n(1,8),
∴
,
解得m=-1,n=-1;
(3)设M(x1,y1),N(x2,y2),
∵
=3
,
=-2
,
即(x1+3,y1+4)=(3,24),(x2+3,y2+4)=(12,6);
∴
,
;
解得
,
;
∴M(0,20),N(9,2);
∴向量
=(9,-18).
| AB |
| a |
| BC |
| b |
| CA |
| c |
∴
| a |
| b |
| c |
∴2
| a |
| b |
| c |
(2)∵
| a |
| b |
| c |
∴(5,-5)=m(-6,-3)+n(1,8),
∴
|
解得m=-1,n=-1;
(3)设M(x1,y1),N(x2,y2),
∵
| CM |
| c |
| CN |
| b |
即(x1+3,y1+4)=(3,24),(x2+3,y2+4)=(12,6);
∴
|
|
解得
|
|
∴M(0,20),N(9,2);
∴向量
| MN |
点评:本题考查了平面向量的线性运算与坐标运算的问题,也考查了向量的相等问题以及解方程组的应用问题,是基础题.

练习册系列答案
相关题目
给出下列命题:
①底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
②若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
③一个棱锥可以有两条侧棱和底面垂直;
④一个棱锥可以有两个侧面和底面垂直;
⑤所有侧面都是正方形的四棱柱一定是正方体.
其中正确的命题是( )
①底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
②若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
③一个棱锥可以有两条侧棱和底面垂直;
④一个棱锥可以有两个侧面和底面垂直;
⑤所有侧面都是正方形的四棱柱一定是正方体.
其中正确的命题是( )
| A、①②③ | B、①③ | C、②③④ | D、④ |
已知a>0,b>0,3是3a与32b等比中项,
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、4 | ||||
B、3+2
| ||||
C、
| ||||
| D、2 |
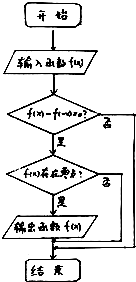 执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )
执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )