题目内容
已知函数f(x)=
-x.
(1)求函数f(x)的值域;
(2)若g(x)=
+x,试判断F(x)=lg
的奇偶性;
(3)若函数y=f(ax)在区间(-1,1)上存在零点,求实数a的范围.
| 1+x |
(1)求函数f(x)的值域;
(2)若g(x)=
| 1-x |
| f(x) |
| g(x) |
(3)若函数y=f(ax)在区间(-1,1)上存在零点,求实数a的范围.
考点:函数奇偶性的判断,函数的值域,函数零点的判定定理
专题:函数的性质及应用
分析:(1)令t=
,t≥0,则x=t2-1,利用换元法,结合二次函数的图象和性质,可得函数的值域;
(2)由已知可得F(x)=lg
=lg(
-x)-lg(
+x),进而可得F(-x)=-F(x),进而根据奇函数的定义,可得:F(x)=lg
为奇函数;
(3)根据函数y=f(ax)在区间(-1,1)上存在零点,可得方程
-ax=0在区间(-1,1)上有根,即方程a2x2-ax-1=0在区间(-1,1)上有根,求出方程的根,构造关于a的不等式,解得实数a的范围.
| 1+x |
(2)由已知可得F(x)=lg
| f(x) |
| g(x) |
| 1+x |
| 1-x |
| f(x) |
| g(x) |
(3)根据函数y=f(ax)在区间(-1,1)上存在零点,可得方程
| 1+ax |
解答:
解:(1)令t=
,t≥0,则x=t2-1,
∴y=f(x)=
-x=-t2+t+1,
当t=
时,函数取最大值
,无最小值,
故函数f(x)的值域为(-∞,
];
(2)∵g(x)=
+x,
∴F(x)=lg
=lg
=lg(
-x)-lg(
+x),
∴F(-x)=lg(
+x)-lg(
-x)=-[lg(
-x)-lg(
+x)=-F(x),
∴F(x)=lg
为奇函数,
(3)函数y=f(ax)在区间(-1,1)上存在零点,
则方程
-ax=0在区间(-1,1)上有根,
即方程1+ax=a2x2在区间(-1,1)上有根,
即方程a2x2-ax-1=0在区间(-1,1)上有根,
即
∈(-1,1),或
∈(-1,1),
解得:a∈(-∞,-
)∪(
,+∞).
| 1+x |
∴y=f(x)=
| 1+x |
当t=
| 1 |
| 2 |
| 5 |
| 4 |
故函数f(x)的值域为(-∞,
| 5 |
| 4 |
(2)∵g(x)=
| 1-x |
∴F(x)=lg
| f(x) |
| g(x) |
| ||
|
| 1+x |
| 1-x |
∴F(-x)=lg(
| 1-x |
| 1+x |
| 1+x |
| 1-x |
∴F(x)=lg
| f(x) |
| g(x) |
(3)函数y=f(ax)在区间(-1,1)上存在零点,
则方程
| 1+ax |
即方程1+ax=a2x2在区间(-1,1)上有根,
即方程a2x2-ax-1=0在区间(-1,1)上有根,
即
1+
| ||
| 2a |
1-
| ||
| 2a |
解得:a∈(-∞,-
| ||
| 2 |
| ||
| 2 |
点评:本题考查的知识点是函数奇偶性的判断,函数的值域,函数零点的判定定理,难度较大,属于难题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
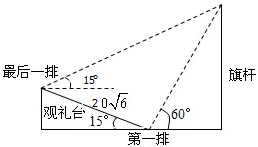 2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一垂直于地面的平面上,在该列的第一排B处和最后一排A处测得旗杆顶端的仰角为15°,且第一排和最后一排的距离为20
2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一垂直于地面的平面上,在该列的第一排B处和最后一排A处测得旗杆顶端的仰角为15°,且第一排和最后一排的距离为20