题目内容
已知sinα=
，则cos2α-cos2α的值为（ ）
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：二倍角的余弦
专题：三角函数的求值
分析：利用体积三角函数的基本关系式求出cos2α，利用二倍角公式化简所求表达式，求解即可．
解答：
解：∵sinα=
，∴cos2α=1-sin2α=1-
=
．
∴cos2α-cos2α=cos2α-2cos2α+1=-
+1=
．
故选：A．
| 3 |
| 5 |
| 9 |
| 25 |
| 16 |
| 25 |
∴cos2α-cos2α=cos2α-2cos2α+1=-
| 16 |
| 25 |
| 9 |
| 25 |
故选：A．
点评：本题考查同角三角函数的基本关系式，二倍角公式的应用，基本知识的考查．
练习册系列答案
相关题目
样本中共有五个个体，其值分别为a，0，1，2，3，若该样本的平均值为1，则样本方差为（ ）
| A、2 | B、2.3 | C、3 | D、3.5 |
若实数x、y满足
，则2x-3y的最值情况是（ ）
|
| A、最大值为2，最小值为-4 |
| B、最大值为2，无最小值 |
| C、无最大值，最小值为-4 |
| D、既无最大值，又无最小值 |
若复数
-1（a为实数，i为虚数单位）是纯虚数，则a=（ ）
| a+i |
| 3+4i |
| A、7 | ||
| B、-7 | ||
C、
| ||
D、-
|
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．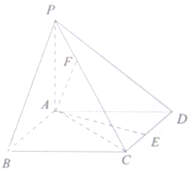
如图，已知四棱锥，底面ABCD为菱形，PA⊥平面ABCD，PA=AB=2，∠ABC=60°，E是CD的中点，F为PC上一点，满足FC=2PF．