题目内容
8.已知集合A={x|-1≤x≤6},B={x|m+1≤x≤3m-1}.(1)若B⊆A,求实数m的取值集合C;
(2)求函数f(x)=x2-2ax+3,x∈C的最小值.
分析 (1)分B是否是空集讨论,从而解得;
(2)结合二次函数的性质及集合C,讨论对称轴,从而求最小值.
解答 解:(1)当B=∅时,m+1>3m-1,所以m<1满足题意;
当B≠∅时,由题意$\left\{{\begin{array}{l}{m+1≤3m-1}\\{m+1≥-1}\\{3m-1≤6}\end{array}}\right.$,解得$1≤m≤\frac{7}{3}$;
综上知:实数m的取集合$C=\{m|m≤\frac{7}{3}\}$
(2)①当$a≥\frac{7}{3}$时,$f{(x)_{min}}=f(\frac{7}{3})=\frac{76-42a}{9}$;
②当a<$\frac{7}{3}$时,$f{(x)_{min}}=f(a)=-{a^2}+3$.
点评 本题考查了集合的化简运算及二次函数的性质的应用,同时考查了分类讨论的思想应用.

练习册系列答案
相关题目
3.变量x,y满足条件$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,求z=2x-3y的最大值和最小值.
16.已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≥3}\\{f(x+1),x<3}\end{array}\right.$,则f(1+log23)的值为( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
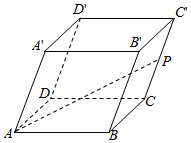 在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.
在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.