题目内容
4.在△ABC中,角A,B,C所对的边分别为a,b,c,且a,b,c依次成等差数列.(Ⅰ)若B=$\frac{π}{6}$,b=1+$\sqrt{3}$,求△ABC的面积;
(Ⅱ)记M=(sinA+sinC)cosB+2$\sqrt{3}{sin^2}$B,求M的取值范围.
分析 (Ⅰ)由等差数列可得a+c=2b,整体代入余弦定理可得ac的值,代入三角形的面积公式可得;
(Ⅱ)由题意和正弦定理可得sinA+sinC=2sinB,代入并化简可得M=$2sin(2B-\frac{π}{3})+\sqrt{3}$,由余弦定理可得B的范围,由三角函数值域可得.
解答 解:(Ⅰ)∵在△ABC中a,b,c依次成等差数列,∴a+c=2b,
∴由余弦定理可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$
=$\frac{(a+c)^{2}-{b}^{2}-2ac}{2ac}$=$\frac{(2b)^{2}-{b}^{2}-2ac}{2ac}$=$\frac{3{b}^{2}}{2ac}$-1,
代入数据可得$\frac{\sqrt{3}}{2}$=$\frac{3(1+\sqrt{3})^{2}}{2ac}$-1,解得ac=6
∴S△ABC=$\frac{1}{2}acsinB=\frac{1}{2}•6•\frac{1}{2}=\frac{3}{2}$;
(Ⅱ)∵a+c=2b,∴由正弦定理可得sinA+sinC=2sinB,
∴M=$(sinA+sinC)cosB+2\sqrt{3}{sin^2}B=2sinBcosB+2\sqrt{3}{sin^2}B=sin2B+\sqrt{3}(1-cos2B)$=$2sin(2B-\frac{π}{3})+\sqrt{3}$,
又$cosB=\frac{{{a^2}+{c^2}-{{(\frac{a+c}{2})}^2}}}{2ac}=\frac{{\frac{3}{4}({a^2}+{c^2})-\frac{ac}{2}}}{2ac}≥\frac{{\frac{3}{4}•2ac-\frac{ac}{2}}}{2ac}=\frac{1}{2}$,
∴$0<B≤\frac{π}{3}$,∴$-\frac{π}{3}<2B-\frac{π}{3}≤\frac{π}{3}$,
∴M=$2sin(2B-\frac{π}{3})+\sqrt{3}∈(0,2\sqrt{3}]$
点评 本题考查正余弦定理解三角形,涉及整体思想和基本不等式求最值,属中档题.

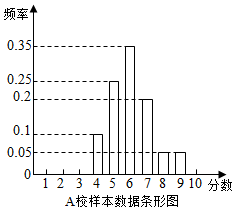 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:B校样本数据统计表
| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(Ⅱ) 记事件C为“A校学生计算机优秀成绩高于B校学生计算机优秀成绩”.假设7分或7分以上为优秀成绩,两校学生计算机成绩相互独立.根据所给样本数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
| A. | (-2,2) | B. | [-2,2] | C. | (-∞,-2) | D. | (2,+∞) |
| A. | 9 | B. | 18 | C. | 19 | D. | 36 |