题目内容
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点左、右分别为F1、F2,点P是双曲线上一点,且$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,P到原点的距离为2,则△PF1F2的面积的取值范围是( )| A. | (0,2) | B. | (1,2) | C. | (2,4) | D. | (0,4) |
分析 由向量垂直可得△PF1F2为直角三角形,由P到原点的距离为2,可得c=2,设P为右支上一点,且|PF2|=t,由双曲线的定义可得|PF1|=2a+t,运用勾股定理和三角形的面积公式,由0<a<2计算即可得到所求范围.
解答 解:由$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,可得△PF1F2为直角三角形,
由P到原点的距离为2,可得c=2,
设P为右支上一点,且|PF2|=t,
由双曲线的定义可得|PF1|=2a+t,
即有t2+(2a+t)2=4c2=16,
即为t2+2at+2a2-8=0,
即t(t+2a)=8-2a2,
又△PF1F2的面积为S=$\frac{1}{2}$|PF1|•PF2|=$\frac{1}{2}$t(2a+t)=4-a2,
由0<a<c=2,可得4-a2∈(0,4).
即有S∈(0,4).
故选:D.
点评 本题考查双曲线的定义和性质,主要是定义法的运用,考查向量垂直的条件和直角三角形的斜边的中线为斜边的一半和勾股定理的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
12.不等式组$\left\{\begin{array}{l}{x+2y≥0}\\{x-3y≥0}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$表示的平面区域的面积为( )
| A. | $\frac{π}{2}$ | B. | $\frac{3}{2}$π | C. | π | D. | 3π |
2.设x,y∈[$\frac{1}{3}$,1],则y+$\frac{x}{\sqrt{4{x}^{2}({y}^{2}+1)-4x+1}}$的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{11}{6}$ |
9.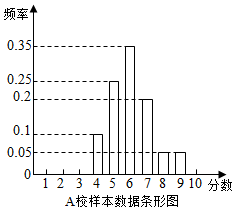 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
B校样本数据统计表
(Ⅰ)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(Ⅱ) 记事件C为“A校学生计算机优秀成绩高于B校学生计算机优秀成绩”.假设7分或7分以上为优秀成绩,两校学生计算机成绩相互独立.根据所给样本数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:B校样本数据统计表
| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(Ⅱ) 记事件C为“A校学生计算机优秀成绩高于B校学生计算机优秀成绩”.假设7分或7分以上为优秀成绩,两校学生计算机成绩相互独立.根据所给样本数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
13.若一组数据x1,x2…xn的方差为9,则数据2x1+1,2x2+1,…2xn+1的方差为( )
| A. | 9 | B. | 18 | C. | 19 | D. | 36 |