题目内容
3.变量x,y满足条件$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,求z=2x-3y的最大值和最小值.分析 作出不等式组对应的平面区域,利用z的几何意义,结合数形结合即可得到结论.
解答 解:由z=2x-3y得y=$\frac{2}{3}x-\frac{z}{3}$,
作出不等式组对应的平面区域如图(阴影部分ABC):
平移直线y=$\frac{2}{3}x-\frac{z}{3}$,由图象可知当直线y=$\frac{2}{3}x-\frac{z}{3}$,过点C时,直线y=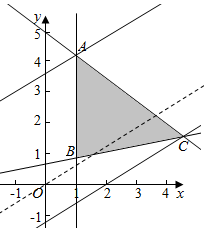 $\frac{2}{3}x-\frac{z}{3}$截距最小,此时z最大,
$\frac{2}{3}x-\frac{z}{3}$截距最小,此时z最大,
由$\left\{\begin{array}{l}{x-4y=-3}\\{3x+5y=25}\end{array}\right.$得$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$,即C(5,2),
代入目标函数z=2x-3y=10-6=4;
当直线y=$\frac{2}{3}x-\frac{z}{3}$,过点A时,直线y=$\frac{2}{3}x-\frac{z}{3}$截距最大,此时z最小,由$\left\{\begin{array}{l}{x=1}\\{3x+5y=25}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=\frac{22}{5}}\end{array}\right.$,
即A(1,$\frac{22}{5}$),
此时z=2×1-3×$\frac{22}{5}$=-$\frac{56}{5}$.
∴目标函数z=2x-3y的最小值是-$\frac{56}{5}$.
点评 本题主要考查线性规划的应用,利用z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
18.函数y=$\sqrt{3}$sin(2x-$\frac{π}{6}$)+2sin2(x-$\frac{π}{12}$)的最小正周期是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 4π |