题目内容
3.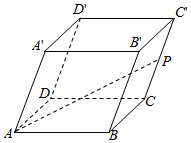 在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.
在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.(Ⅰ)用$\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AA'}$表示$\overrightarrow{AP}$;
(Ⅱ)求AP的长.
分析 (Ⅰ)根据向量加法、数乘的几何意义和相等向量的概念便可以得出$\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AA′}$;
(Ⅱ)根据(Ⅰ)${\overrightarrow{AP}}^{2}=(\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AA′})^{2}$,这样根据条件进行数量积的计算便可求出${\overrightarrow{AP}}^{2}$的值,从而便可得出AP的长度.
解答 解:(Ⅰ)$\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CP}$
=$\overrightarrow{AB}+\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CC′}$
=$\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AA′}$;
(Ⅱ)根据条件,${\overrightarrow{AP}}^{2}=(\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AA′})^{2}$
=${\overrightarrow{AB}}^{2}+{\overrightarrow{AD}}^{2}+\frac{1}{4}{\overrightarrow{AA′}}^{2}+2\overrightarrow{AB}•\overrightarrow{AD}$$+\overrightarrow{AB}•\overrightarrow{AA′}+\overrightarrow{AD}•\overrightarrow{AA′}$
=16+36+16+0+16+24
=108;
∴$|\overrightarrow{AP}|=6\sqrt{3}$.
点评 考查向量的加法和数乘的几何意义,相等向量的概念,以及数量积的运算及计算公式,要求$|\overrightarrow{AP}|$而求${\overrightarrow{AP}}^{2}$的方法.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 4π |
| A. | {x|0<x<1} | B. | {x|0≤x≤1} | C. | {x|x≤1} | D. | {x|x≥0} |
| A. | a=1,b=2 | B. | a=2,b=1 | C. | a=-1,b=2 | D. | a=2,b=-1 |
| A. | $\frac{π}{2}$ | B. | $\frac{3}{2}$π | C. | π | D. | 3π |
| A. | (-2,2) | B. | [-2,2] | C. | (-∞,-2) | D. | (2,+∞) |