题目内容
13.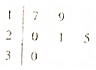 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.(Ⅰ)根据茎叶图计算样本均值;
(Ⅱ)日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人?
(Ⅲ)在(Ⅱ)的条件下,从该车间12名工人中,任取3人,求恰有1名优秀工人的情况有多少种?
分析 (1)由茎叶图能求出样本均值.
(2)求出样本中优秀工人占的比例,由此能推断该车间12名工人中有多少名优秀工人.
(3)利用组合数公式能求出从该车间12名工人中,任取3人,恰有1名优秀工人的情况有多少种.
解答 解:(1)样本均值为$\frac{17+19+20+21+25+30}{6}=\frac{132}{6}=22$.…(4分)
(2)由(1)知样本中优秀工人占的比例为$\frac{2}{6}=\frac{1}{3}$,
故推断该车间12名工人中有$12×\frac{1}{3}=4$名优秀工人.…(8分)
(3)从该车间12名工人中,任取3人,恰有1名优秀工人,
则恰有1名优秀工人的情况有$c_4^1c_8^2=112$种.…(12分)
点评 本题考查样本均值、优秀工人个数、不同的抽样种数的求法,是基础题,解题时要认真审题,注意茎叶图性质的合理运用.

练习册系列答案
相关题目
8.已知函数f(x)=$\sqrt{3}$sin2x-cos2x+1,下列结论中错误的是( )
| A. | f(x)的图象关于($\frac{π}{12}$,1)中心对称 | B. | f(x)在($\frac{5π}{12}$,$\frac{11π}{12}$)上单调递减 | ||
| C. | f(x)的图象关于x=$\frac{π}{3}$对称 | D. | f(x)的最大值为3 |
18.已知集合 A={-2,-1,0,2,3},B={y|y=|x|,x∈A},则A∩B=( )
| A. | {0,1,2,3} | B. | {2,3} | C. | {0,1,2} | D. | {0,2,3} |
3.若二次函数f(x)=cx2+4x+a(x∈R)的值域为[0,+∞),则$\frac{1}{a}$+$\frac{9}{c}$的最小值为( )
| A. | 3 | B. | $\frac{9}{2}$ | C. | 5 | D. | 7 |
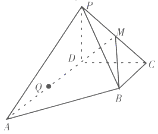 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4