题目内容
18．
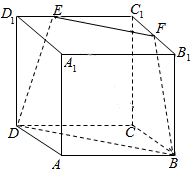如图，在棱长为6的正方体ABCD-A1B1C1D1中，E，F分别在C1D1与C1B1上，且C1E=4，C1F=3，连接EF，FB，DE，BD，则几何体EFC1-DBC的体积为（ ）| A． | 66 | B． | 68 | C． | 70 | D． | 72 |
分析 直接利用等积法把几何体EFC1-DBC的体积转化为两个棱锥的体积求解．
解答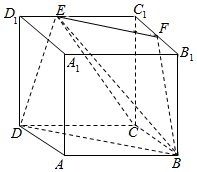 
解：如图
∵ABCD-A1B1C1D1是边长为6的正方体，
且C1E=4，C1F=3，
∴${S}_{BC{C}_{1}F}=\frac{1}{2}（3+6）×6=27$，${S}_{△BCD}=\frac{1}{2}×6×6=18$，
则几何体EFC1-DBC的体积等于${V}_{E-ABC}+{V}_{E-BC{C}_{1}F}$$\frac{1}{3}×27×4+\frac{1}{3}×18×6=72$．
故选：D．
点评 本题考查棱柱、棱锥、棱台体积的求法，考查了等积法在求解几何体体积中的运用，是中档题．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
10．在△ABC中，若$\frac{AC}{AB}$=$\frac{cosB}{cosC}$，则（ ）
| A． | A=C | B． | A=B | C． | B=C | D． | 以上都不正确 |