题目内容
3.在△ABC中,a、b、c分别为角A、B、C所对的边,若$\frac{a}{cos\frac{A}{2}}$=$\frac{b}{cos\frac{B}{2}}$=$\frac{c}{cos\frac{C}{2}}$,则此三角形的形状为等边三角形.分析 $\frac{a}{cos\frac{A}{2}}$=$\frac{b}{cos\frac{B}{2}}$=$\frac{c}{cos\frac{C}{2}}$,由正弦定理可得:$\frac{sinA}{cos\frac{A}{2}}$=$\frac{sinB}{cos\frac{B}{2}}$=$\frac{sinC}{cos\frac{C}{2}}$,再利用倍角公式可得;$sin\frac{A}{2}$=$sin\frac{B}{2}$=$sin\frac{C}{2}$.再利用三角函数的单调性即可得出.
解答 解:在△ABC中,∵$\frac{a}{cos\frac{A}{2}}$=$\frac{b}{cos\frac{B}{2}}$=$\frac{c}{cos\frac{C}{2}}$,由正弦定理可得:$\frac{sinA}{cos\frac{A}{2}}$=$\frac{sinB}{cos\frac{B}{2}}$=$\frac{sinC}{cos\frac{C}{2}}$,∴$sin\frac{A}{2}$=$sin\frac{B}{2}$=$sin\frac{C}{2}$.
∵$\frac{A}{2}$,$\frac{B}{2}$,$\frac{C}{2}$∈$(0,\frac{π}{2})$,
∴$\frac{A}{2}=\frac{B}{2}=\frac{C}{2}$,即A=B=C.
∴△ABC是等边三角形.
故答案为:等边三角形.
点评 本题考查了正弦定理、倍角公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知向量$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(0,1),则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 4 |
18.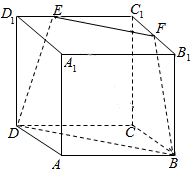 如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( )
如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( )
 如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( )
如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( )| A. | 66 | B. | 68 | C. | 70 | D. | 72 |
15.已知在等比数列{an}中,a1+a2+a3=6,a1+a3+a5=10.5,则公比q( )
| A. | -$\frac{1}{2}$或$\frac{3}{2}$ | B. | $\frac{1}{2}$或-$\frac{3}{2}$ | C. | 1或-3 | D. | -1或3 |
6.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,过点F作x轴的垂线交双曲线的右支于C,D两点,与双曲线的渐近线交于点P,点C和点P在第-象限,点D在第四象限,若|PC|=|CD|,则该双曲线的离心率为( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{9}{8}$ |
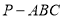 中,
中,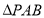 和
和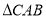 都是以
都是以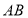 为斜边的等腰直角三角形.
为斜边的等腰直角三角形.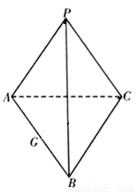
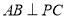 ;
;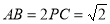 ,求三棱锥
,求三棱锥