题目内容
12.若(ax+$\frac{1}{x}$)(2x+$\frac{1}{x}$)5展开式中的常数项为-40,则a=-3.分析 根据题意,(ax+$\frac{1}{x}$)(2x+$\frac{1}{x}$)5展开式中的常数项,是(2x+$\frac{1}{x}$)5的展开式中$\frac{1}{x}$项的系数与ax的系数之积,
再加上x项的系数与$\frac{1}{x}$的系数的积,利用(2x+$\frac{1}{x}$)5展开式的通项公式,求出展开式中含$\frac{1}{x}$与x项的系数,列出方程求出a的值.
解答 解:(ax+$\frac{1}{x}$)(2x+$\frac{1}{x}$)5展开式中的常数项,
是(2x+$\frac{1}{x}$)5的展开式中$\frac{1}{x}$项的系数与ax的系数之积,
再加上x项的系数与$\frac{1}{x}$的系数的积;
又(2x+$\frac{1}{x}$)5展开式的通项公式为:
Tr+1=${C}_{5}^{r}$•(2x)5-r•${(\frac{1}{x})}^{r}$=25-r•${C}_{5}^{r}$•x5-2r,
令5-2r=-1,解得r=3,
∴T3+1=22•${C}_{5}^{3}$•$\frac{1}{x}$=40•$\frac{1}{x}$;
令5-2r=1,解得r=2,
∴T2+1=23•${C}_{5}^{2}$•x=80•x;
∴展开式中的常数项为:
40a+80=-40,
解得a=-3.
故答案为:-3.
点评 本题考查了二项式系数性质的应用问题,熟练掌握二次项系数的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.2015年秋季开学之际,某校高一数学老师为了解学生的计算能力,先给出了一组计算测试题,全校学生完成时间在[20,40)(单位:分钟),各区间学生频率如下表:
若全校共有高一新生1000人.
(1)若学校规定完成时间不低于30分钟的要进行强化训练,试试估计全校参加强化训练的学生人数;
(2)若从全校按照完成时间,利用分层抽样的方法抽取10人.
①若从抽取的这10人中随机抽取1人,求他完成时间恰好在[30,40)的概率;
②若一节课为45分钟,从开始上课即进行测试,从这10人中随机抽取2人,求这两人所用测试时间都不超过30分钟的概率.
| 完成时间 | 频率 |
| [20,25) | 0.2 |
| [25,30) | 0.5 |
| [30,35) | 0.2 |
| [35,40) | 0.1 |
(1)若学校规定完成时间不低于30分钟的要进行强化训练,试试估计全校参加强化训练的学生人数;
(2)若从全校按照完成时间,利用分层抽样的方法抽取10人.
①若从抽取的这10人中随机抽取1人,求他完成时间恰好在[30,40)的概率;
②若一节课为45分钟,从开始上课即进行测试,从这10人中随机抽取2人,求这两人所用测试时间都不超过30分钟的概率.
1.(5)若xy满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{y+2≥0}\\{x+y+2≤0}\end{array}\right.$,则$\frac{y+1}{x-1}$的取值范围为( )
| A. | [-$\frac{1}{3}$,$\frac{1}{5}$] | B. | [-$\frac{1}{3}$,1] | C. | (-∞,-$\frac{1}{3}$]∪[$\frac{1}{5}$,+∞) | D. | (-∞,-$\frac{1}{3}$]∪[1,+∞) |
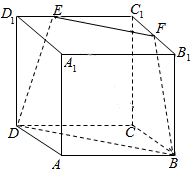 如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( )
如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( ) 与圆
与圆 的位置关系为( )
的位置关系为( )