题目内容
7．设集合A={x|x2-3x-4≥0}，集合B={x||x-2|＜4}，求A∩B．分析 分别求解一元二次不等式和绝对值不等式化简集合A，B，取交集得答案．
解答 解：由x2-3x-4≥0，得x＜-1或x＞4，
∴A={x|x2-3x-4≥0}={x|x＜-1或x＞4}，
B={x||x-2|＜4}={x|-2＜x＜6}，
∴A∩B={x|x＜-1或x＞4}∩{x|-2＜x＜6}=（-2，-1）∪（4，6）．
点评 本题考查交集及其运算，考查了一元二次不等式和绝对值不等式的解法，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
18．
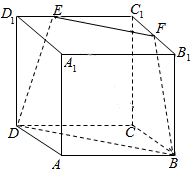如图，在棱长为6的正方体ABCD-A1B1C1D1中，E，F分别在C1D1与C1B1上，且C1E=4，C1F=3，连接EF，FB，DE，BD，则几何体EFC1-DBC的体积为（ ）
如图，在棱长为6的正方体ABCD-A1B1C1D1中，E，F分别在C1D1与C1B1上，且C1E=4，C1F=3，连接EF，FB，DE，BD，则几何体EFC1-DBC的体积为（ ）| A． | 66 | B． | 68 | C． | 70 | D． | 72 |
15．已知在等比数列{an}中，a1+a2+a3=6，a1+a3+a5=10.5，则公比q（ ）
| A． | -$\frac{1}{2}$或$\frac{3}{2}$ | B． | $\frac{1}{2}$或-$\frac{3}{2}$ | C． | 1或-3 | D． | -1或3 |
与圆
的位置关系为（ ）