题目内容
13.函数y=x2-2的增区间为[0,+∞).分析 根据二次函数的单调性或二次函数y=x2-2的图象便可写出该函数的增区间.
解答 解:二次函数y=x2-2在[0,+∞)上单调递增;
∴该函数的增区间为[0,+∞).
故答案为:[0,+∞).
点评 考查二次函数的单调性,要熟悉二次函数y=x2-2的图象,以及根据函数图象求函数单调区间的方法.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
6.已知集合A={x|y=$\sqrt{x-4}$},B={x|-1≤2x-1≤0},则∁RA∩B=( )
| A. | (4,+∞) | B. | [0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,4] | D. | (1,4) |
4.2015年秋季开学之际,某校高一数学老师为了解学生的计算能力,先给出了一组计算测试题,全校学生完成时间在[20,40)(单位:分钟),各区间学生频率如下表:
若全校共有高一新生1000人.
(1)若学校规定完成时间不低于30分钟的要进行强化训练,试试估计全校参加强化训练的学生人数;
(2)若从全校按照完成时间,利用分层抽样的方法抽取10人.
①若从抽取的这10人中随机抽取1人,求他完成时间恰好在[30,40)的概率;
②若一节课为45分钟,从开始上课即进行测试,从这10人中随机抽取2人,求这两人所用测试时间都不超过30分钟的概率.
| 完成时间 | 频率 |
| [20,25) | 0.2 |
| [25,30) | 0.5 |
| [30,35) | 0.2 |
| [35,40) | 0.1 |
(1)若学校规定完成时间不低于30分钟的要进行强化训练,试试估计全校参加强化训练的学生人数;
(2)若从全校按照完成时间,利用分层抽样的方法抽取10人.
①若从抽取的这10人中随机抽取1人,求他完成时间恰好在[30,40)的概率;
②若一节课为45分钟,从开始上课即进行测试,从这10人中随机抽取2人,求这两人所用测试时间都不超过30分钟的概率.
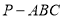 中,
中,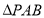 和
和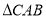 都是以
都是以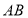 为斜边的等腰直角三角形.
为斜边的等腰直角三角形.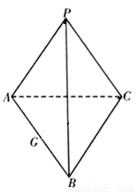
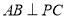 ;
;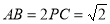 ,求三棱锥
,求三棱锥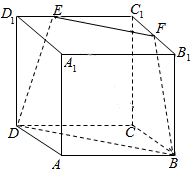 如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( )
如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( )