题目内容
9.在△ABC中,角A,B,C所对的边分别为a,b,c,若sinA=$\frac{2}{3}$,sinB=2cosC且c2-a2=b,则b=3.分析 由c2-a2=b,可得c>a,A为锐角,利用同角三角函数基本关系式可求cosA=$\frac{\sqrt{5}}{3}$,利用余弦定理可求$\frac{b+1}{2c}$=$\frac{\sqrt{5}}{3}$,根据两角和的正弦函数公式,同角三角函数基本关系式进而可求tanC=$\frac{sinC}{cosC}$=$\frac{4}{\sqrt{5}}$,从而由正弦定理可得$\frac{b}{c}$=$\frac{2}{tanC}$=$\frac{\sqrt{5}}{2}$,联立即可解得b的值.
解答 解:∵c2-a2=b,可得:c2=a2+b,即c>a,
∴A为锐角,
∵sinA=$\frac{2}{3}$,
∴cosA=$\sqrt{1-si{n}^{2}A}$=$\frac{\sqrt{5}}{3}$,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{{b}^{2}+b}{2bc}$=$\frac{b+1}{2c}$=$\frac{\sqrt{5}}{3}$,①
∵sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{2}{3}$cosC+$\frac{\sqrt{5}}{3}$sinC=2cosC,
可得:tanC=$\frac{sinC}{cosC}$=$\frac{4}{\sqrt{5}}$,
∴$\frac{b}{c}$=$\frac{sinB}{sinC}$=$\frac{2cosC}{sinC}$=$\frac{2}{tanC}$=$\frac{\sqrt{5}}{2}$,②
由①②可得b=3.
故答案为:3.
点评 本题主要考查了同角三角函数基本关系式,余弦定理,两角和的正弦函数公式,同角三角函数基本关系式,正弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $-\frac{1}{7}$ | B. | 7 | C. | $\frac{1}{7}$ | D. | -7 |
| A. | [-2$\sqrt{5}$,-4] | B. | (-2$\sqrt{5}$,-4] | C. | [-2$\sqrt{5}$,-4) | D. | (-2$\sqrt{5}$,-4) |
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |

| A. | 9道 | B. | 8道 | C. | 7道 | D. | 6道 |
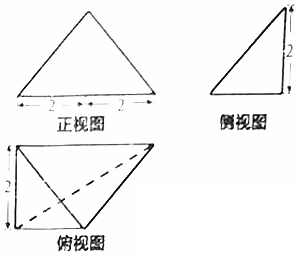
| A. | 4 | B. | $2\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $4\sqrt{2}$ |