题目内容
4.已知直线l:y=2x+m与曲线y=-$\sqrt{4-{x}^{2}}$有两个公共点,则实数m的取值范围是( )| A. | [-2$\sqrt{5}$,-4] | B. | (-2$\sqrt{5}$,-4] | C. | [-2$\sqrt{5}$,-4) | D. | (-2$\sqrt{5}$,-4) |
分析 作出图象,根据直线与圆的位置关系得出m的临界值,从而得出m的范围.
解答 解:曲线y=-$\sqrt{4-{x}^{2}}$表示以(0,0)为圆心,以2为半径的下半圆,
作出图形如图所示:
∵直线l:y=2x+m与半圆有两个公共点,
∴当直线l经过点(2,0)时,m取得最大值-4,
当直线l与半圆相切时,圆心(0,0)到直线l的距离为2,
即$\frac{|m|}{\sqrt{5}}$=2,∴m=2$\sqrt{5}$(舍)或m=-2$\sqrt{5}$.
∴-2$\sqrt{5}$<m≤-4.
故选B.
点评 本题考查了直线与圆的位置关系,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
19.若函数$f(x)=\left\{\begin{array}{l}{a^x},x>1\\(4-\frac{a}{2})x+2,x≤1\end{array}\right.$在(-∞,+∞)上单调递增,则的取值范围是( )
| A. | [4,8) | B. | (1,+∞) | C. | (4,8) | D. | (1,8) |
16.设函数f(x)满足2x2f(x)+x3f′(x)=ex,f(2)=$\frac{{e}^{2}}{8}$,则x∈[2,+∞)时,f(x)( )
| A. | 有最大值$\frac{{e}^{2}}{8}$ | B. | 有最小值$\frac{{e}^{2}}{8}$ | C. | 有最大值$\frac{{e}^{2}}{2}$ | D. | 有最小值$\frac{{e}^{2}}{2}$ |
3.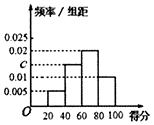 某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
(Ⅰ)求a,b,c的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中选取5人进行座谈.现再从这5人中任选2人,求这两人都合格的概率.
 某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.| 等级 | 不合格 | 合格 | ||
| 得分 | [20,40) | [40,60) | [60,80) | [80,100] |
| 频数 | 6 | a | 24 | b |
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中选取5人进行座谈.现再从这5人中任选2人,求这两人都合格的概率.
 如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.
如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.