题目内容
4.已知$θ∈({\frac{π}{2},π}),\;\;sinθ=\frac{3}{5}$,则$tan({θ+\frac{π}{4}})=({\;\;\;\;\;\;})$.| A. | $-\frac{1}{7}$ | B. | 7 | C. | $\frac{1}{7}$ | D. | -7 |
分析 利用同角三角函数的基本关系求得cosθ的值,可得tanθ的值,再利用两角差的正切公式,求得要求式子的值.
解答 解:已知$θ∈({\frac{π}{2},π}),\;\;sinθ=\frac{3}{5}$,∴cosθ=-$\sqrt{{1-sin}^{2}θ}$=-$\frac{4}{5}$,∴tanθ=$\frac{sinθ}{cosθ}$=-$\frac{3}{4}$,
∴tan($θ+\frac{π}{4}$)=$\frac{1+tanθ}{1-tanθ}$=$\frac{1}{7}$,
故选:C.
点评 本题主要考查同角三角函数的基本关系,两角差的正切公式的应用,属于基础题.

练习册系列答案
相关题目
12.已知双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$上有不共线三点A,B,C,且AB,BC,AC的中点分别为D,E,F,若满足OD,OE,OF的斜率之和为-1,则$\frac{1}{{{k_{AB}}}}+\frac{1}{{{k_{BC}}}}+\frac{1}{{{k_{AC}}}}$=( )
| A. | 2 | B. | $-\sqrt{3}$ | C. | -2 | D. | 3 |
19.若函数$f(x)=\left\{\begin{array}{l}{a^x},x>1\\(4-\frac{a}{2})x+2,x≤1\end{array}\right.$在(-∞,+∞)上单调递增,则的取值范围是( )
| A. | [4,8) | B. | (1,+∞) | C. | (4,8) | D. | (1,8) |
16.设函数f(x)满足2x2f(x)+x3f′(x)=ex,f(2)=$\frac{{e}^{2}}{8}$,则x∈[2,+∞)时,f(x)( )
| A. | 有最大值$\frac{{e}^{2}}{8}$ | B. | 有最小值$\frac{{e}^{2}}{8}$ | C. | 有最大值$\frac{{e}^{2}}{2}$ | D. | 有最小值$\frac{{e}^{2}}{2}$ |
10.已知四棱锥的三视图如图所示,则该四棱锥的全面积为( )
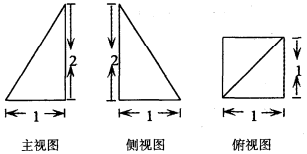

| A. | 4 | B. | 5 | C. | $2+\sqrt{5}$ | D. | $3+\sqrt{5}$ |