题目内容
求过直线x+3y-7=0与已知圆x2+y2+2x-2y-3=0的交点，且在两坐标轴上的四个截距之和为8的圆的方程．
考点：直线和圆的方程的应用
专题：综合题,直线与圆
分析：设x2+y2+2x-2y-3+λ（x+3y-7）=0，分别求出在x、y轴上的截距之和，利用在两坐标轴上的四个截距之和为8，求出λ，即可求出圆的方程．
解答：
解：设x2+y2+2x-2y-3+λ（x+3y-7）=0
令y=0，∴x2+（2+λ）x-3-7λ=0
∴在x轴上的截距之和为-2-λ．
同理：在y轴上的截距之和为2-3λ，
∵在两坐标轴上的四个截距之和为8
∴-2-λ+2-3λ=8，
∴λ=-2
∴圆的方程为x2+y2-8y+11=0．
令y=0，∴x2+（2+λ）x-3-7λ=0
∴在x轴上的截距之和为-2-λ．
同理：在y轴上的截距之和为2-3λ，
∵在两坐标轴上的四个截距之和为8
∴-2-λ+2-3λ=8，
∴λ=-2
∴圆的方程为x2+y2-8y+11=0．
点评：本题考查直线与圆的位置关系，考查韦达定理的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
以下不等式不正确的是（ ）
A、tan（-
| ||||
B、sin（-
| ||||
C、cos（-
| ||||
D、tan（-
|
由正数组成的等比数列{an}满足：a4a8=9，则a5，a7的等比中项为（ ）
| A、±3 | B、3 | C、±9 | D、9 |
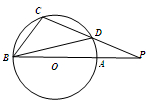如图，AB是半径为3的⊙O的直径，CD是弦，BA，CD的延长线交于点P，PA=4，PD=5，则∠CBD=