题目内容
已知圆C:x2+y2-4x-4y=0,直线l:
x+y+6-2
=0,在圆C上任取一点A,则点A到直线l的距离小于2的概率为 .
| 3 |
| 3 |
考点:几何概型
专题:概率与统计
分析:求出圆的标准方程,利用点到直线的距离公式确定点A的位置即可得到结论.
解答:
解:圆的标准方程为(x-2)2+(y-2)2=8,圆心C(2,2),半径r=2
,
则圆心到直线的距离d=
=
=4>r=2
,
和直线距离等于2的直线设为
x+y+b=0,
则
=2,解得b=10-2
(舍去)或b=2-2
,
作出对应的直线
x+y+2-2
=0,
如图:则圆心到直线
x+y+2-2
=0的距离为4-2=2,
此时点A位于B,D,此时∠DCB=90°,
则满足点A到直线l的距离小于2的点A,位于弧BD上,
对应的概率为
=
,
故答案为:
| 2 |
则圆心到直线的距离d=
|2
| ||||
|
| 8 |
| 2 |
| 2 |
和直线距离等于2的直线设为
| 3 |
则
|6-2
| ||
| 2 |
| 3 |
| 3 |
作出对应的直线
| 3 |
| 3 |
如图:则圆心到直线
| 3 |
| 3 |
此时点A位于B,D,此时∠DCB=90°,
则满足点A到直线l的距离小于2的点A,位于弧BD上,
对应的概率为
| 90° |
| 360° |
| 1 |
| 4 |
故答案为:

| 1 |
| 4 |
点评:本题主要考查几何槪型的概率的计算,利用直线和圆的位置公式以及点到直线的距离公式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等比数列{an}中,a1=27,a4=a3a5,则a6=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={1,2,4},B={y|y=log2x,x∈A},则A∪B=( )
| A、{0,1,2} |
| B、{1,2} |
| C、{0,1,2,4} |
| D、{0,1,4} |
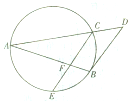 如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且
如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且