题目内容
设函数f(x)=lnx-
ax2-bx.
(Ⅰ)当a=b=
时,求函数f(x)的最大值;
(Ⅱ)令F(x)=f(x)+
ax2+bx+
(0<x≤3)其图象上任意一点P(x0,y0)处切线的斜率k≤
恒成立,求实数a的取值范围;
(Ⅲ)当a=0,b=-1,方程2mf(x)=x2有唯一实数解,求正数m的值.
| 1 |
| 2 |
(Ⅰ)当a=b=
| 1 |
| 2 |
(Ⅱ)令F(x)=f(x)+
| 1 |
| 2 |
| a |
| x |
| 1 |
| 2 |
(Ⅲ)当a=0,b=-1,方程2mf(x)=x2有唯一实数解,求正数m的值.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)利用导数求得函数的最大值即可;
(Ⅱ)由导数的几何意义求得切线的斜率,解不等式求得a的取值范围;
(Ⅲ)构造函数g(x)=x2-2mlnx-2mx,方程2mf(x)=x2有唯一实数解,等价于函数g(x)的最小值等于0,利用导数求得函数g(x)的最小值,解得即可.
(Ⅱ)由导数的几何意义求得切线的斜率,解不等式求得a的取值范围;
(Ⅲ)构造函数g(x)=x2-2mlnx-2mx,方程2mf(x)=x2有唯一实数解,等价于函数g(x)的最小值等于0,利用导数求得函数g(x)的最小值,解得即可.
解答:
解:(Ⅰ)依题意,知f(x)的定义域为(0,+∞),
当a=b=
时,f(x)=lnx-
x2-
x,
令f′(x)=
-
x-
=
=0 …(2分)
解得x=1.
因为g(x)=0有唯一解,所以g(x2)=0,当0<x<1时,f'(x)>0,此时f(x)单调递增;
当x>1时,f'(x)<0,此时f(x)单调递减.
所以f(x)的极大值为f(1)=-
,此即为最大值 …(4分)
(Ⅱ)F(x)=lnx+
,x∈(0,3],则有k=F′(x0)=
≤
,在x0∈(0,3]上恒成立,
所以a≥(-
+x0)max,x0∈(0,3]
当x0=1时,-
+x0取得最大值
,所以a≥
…(8分)
(Ⅲ)因为方程2mf(x)=x2有唯一实数解,所以x2-2mlnx-2mx=0有唯一实数解,
设g(x)=x2-2mlnx-2mx,则g′(x)=
.
令g'(x)=0,x2-mx-m=0
因为m>0,x>0,所以x1=
<0(舍去),x2=
,
当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)上单调递减,
当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)上单调递增,
当x=x2时,g'(x2)=0,g(x)取最小值g(x2).…(10分)
则
即
所以2mlnx2+mx2-m=0,
因为m>0,所以2lnx2+x2-1=0(*)
设函数h(x)=2lnx+x-1,
因为当x>0时,h(x)是增函数,所以h(x)=0至多有一解.
所以h(1)=0,所以方程(*)的解为x2=1,即
=1,解得m=
…(12分)
当a=b=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
令f′(x)=
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| -(x+2)(x-1) |
| 2x |
解得x=1.
因为g(x)=0有唯一解,所以g(x2)=0,当0<x<1时,f'(x)>0,此时f(x)单调递增;
当x>1时,f'(x)<0,此时f(x)单调递减.
所以f(x)的极大值为f(1)=-
| 3 |
| 4 |
(Ⅱ)F(x)=lnx+
| a |
| x |
| x0-a |
| x02 |
| 1 |
| 2 |
所以a≥(-
| 1 |
| 2 |
| x | 2 0 |
当x0=1时,-
| 1 |
| 2 |
| x | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅲ)因为方程2mf(x)=x2有唯一实数解,所以x2-2mlnx-2mx=0有唯一实数解,
设g(x)=x2-2mlnx-2mx,则g′(x)=
| 2x2-2mx-2m |
| x |
令g'(x)=0,x2-mx-m=0
因为m>0,x>0,所以x1=
m-
| ||
| 2 |
m+
| ||
| 2 |
当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)上单调递减,
当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)上单调递增,
当x=x2时,g'(x2)=0,g(x)取最小值g(x2).…(10分)
则
|
|
所以2mlnx2+mx2-m=0,
因为m>0,所以2lnx2+x2-1=0(*)
设函数h(x)=2lnx+x-1,
因为当x>0时,h(x)是增函数,所以h(x)=0至多有一解.
所以h(1)=0,所以方程(*)的解为x2=1,即
m+
| ||
| 2 |
| 1 |
| 2 |
点评:本题主要考查利用导数研究函数的单调性,求切线方程,求函数的最值等知识,注意恒成立问题的转化及构造法的运用,综合性强,属难题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
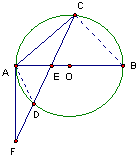 如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=
如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=