题目内容
3.直线l的方程为$|{\begin{array}{l}1&0&2\\ x&2&3\\ y&{-1}&2\end{array}}|=0$,则直线l的一个法向量是( )| A. | (1,2) | B. | (2,1) | C. | (-1,2) | D. | (2,-1) |
分析 直线l的方程为$|{\begin{array}{l}1&0&2\\ x&2&3\\ y&{-1}&2\end{array}}|=0$,化为:2x+4y-7=0,利用相互垂直的直线斜率之间的关系即可得出.
解答 解:直线l的方程为$|{\begin{array}{l}1&0&2\\ x&2&3\\ y&{-1}&2\end{array}}|=0$,化为:2x+4y-7=0,
k=-2.
设直线l的一个法向量为$\overrightarrow{n}$=(m,n),
则$\frac{n}{m}$×(-2)=-1,可得:m=2n.
则直线l的一个法向量是(1,2).
故选:A.
点评 本题考查了相互垂直的直线斜率之间的关系、行列式的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
13.“x>-2”是“x2<4”( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.小品类是春节文艺晚会的重要节目,一调查机构为研究“喜欢收看春节文艺晚会小品类节目与地域文化是否有关”,在南北方不同地域随机抽取了100名市民进行调查,发现被调查对象的北方人有40名喜欢收看,有15名不喜欢收看;调查对象的南方人有20名喜欢收看,有25名不喜欢收看
(1)在被调查对象中,喜欢收看春节文艺晚会小品类节目的人数占各自地域的比例分别是多少?并初步判断喜欢收看春节文艺晚会小品类节目与地域是否有关?
(2)试根据题设数据完成2X2列联表,并判断是否有99.5%的把握认为喜欢收看春节文艺晚会小品类节目与地域文化有关
参考数据公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},n=a+b+c+d$
临界值:
(1)在被调查对象中,喜欢收看春节文艺晚会小品类节目的人数占各自地域的比例分别是多少?并初步判断喜欢收看春节文艺晚会小品类节目与地域是否有关?
(2)试根据题设数据完成2X2列联表,并判断是否有99.5%的把握认为喜欢收看春节文艺晚会小品类节目与地域文化有关
参考数据公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},n=a+b+c+d$
临界值:
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
11.如图下面程序框图运行的结果s=1320,那么判断框中应填入( )


| A. | k<10? | B. | k>10? | C. | k<11? | D. | k>11? |
18.函数f(x)的定义域为[-1,1],图象如图1所示:函数g(x)的定义域为[-2,2],图象如图2所示,方程f[g(x)]=0有m个实数根,方程g[f(x)]=0有n个实数根,则m+n=( )
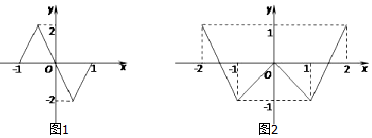

| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
8. 如图,网格纸上的小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积是( )
如图,网格纸上的小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积是( )
 如图,网格纸上的小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积是( )
如图,网格纸上的小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积是( )| A. | 4+6π | B. | 4+12π | C. | 8+6π | D. | 8+12π |
15.定义一种运算a?b=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$,若f(x)=2x?|x2-4x+3|,当g(x)=f(x)-m有5个零点时,则实数m的取值范围是( )
| A. | (0,1) | B. | [0,1] | C. | (1,3) | D. | [1,3] |
12.某条公共汽车线路收支差额y与乘客量x的函数关系如图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
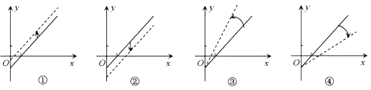

| A. | ①反映了建议(Ⅱ),③反映了建议(Ⅰ) | B. | ①反映了建议(Ⅰ),③反映了建议(Ⅱ) | ||
| C. | ②反映了建议(Ⅰ),④反映了建议(Ⅱ) | D. | ④反映了建议(Ⅰ),②反映了建议(Ⅱ) |
13.已知向量$\overrightarrow a=(-2,0),\overrightarrow a-\overrightarrow b=(-3,-1)$,则下列结论正确的是 ( )
| A. | $\overrightarrow a•\overrightarrow b=2$ | B. | $\overrightarrow a∥\overrightarrow b$ | C. | $|\overrightarrow a|=|\overrightarrow b|$ | D. | $\overrightarrow b⊥(\overrightarrow a+\overrightarrow b)$ |