题目内容
8．
如图，网格纸上的小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积是（ ）| A． | 4+6π | B． | 4+12π | C． | 8+6π | D． | 8+12π |
分析 根据三视图知几何体是组合体：下面是半个圆柱、上面是一个以圆柱轴截面为底的四棱锥，并求出圆柱的底面半径、母线，四棱锥的高和底面边长，代入体积公式求值即可．
解答 解：根据三视图知几何体是组合体，
下面是半个圆柱、上面是一个以圆柱轴截面为底的四棱锥，
圆柱的底面半径为2，母线长为3；四棱锥的高是2，底面是边长为4、3的矩形，
∴该几何体的体积V=$\frac{1}{2}×π×{2}^{2}×3+\frac{1}{3}×3×4×2$=6π+8，
故选：B．
点评 本题考查由三视图求几何体的体积，以及几何体的体积公式，考查空间想象能力，三视图正确复原几何体是解题的关键．
练习册系列答案
相关题目
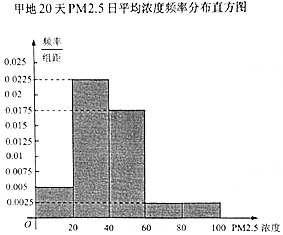
18．为检测空气质量，某市环保局随机抽取了甲、乙两地2016年20天PM2.5日平均浓度（单位：微克/立方米）监测数据，得到甲地PM2.5日平均浓度频率分布直方图和乙地PM2.5日平均浓度的频数分布表．
乙地20天PM2.5日平均浓度频数分布表
（1）根据乙地20天PM2.5日平均浓度的频率分布表，作出作出相应的频率分组直方图，并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度（不要求计算出具体值，给出结论即可）；
（2）通过调查，该市市民对空气质量的满意度从高到低分为三个等级：
从乙地这20天PM2.5日平均浓度不超过40的天数中随机抽取两天，求这两天中至少有一天居民对空气质量满意度为“非常满意”的概率．
乙地20天PM2.5日平均浓度频数分布表
| PM2.5日平均浓度（微克/立方米） | [0，20] | （20，40] | （40，60] | （60，80] | （80，100] |
| 频数（天） | 2 | 3 | 4 | 6 | 5 |
（2）通过调查，该市市民对空气质量的满意度从高到低分为三个等级：
| 满意度等级 | 非常满意 | 满意 | 不满意 |
| PM2.5日平均浓度（微克/立方米） | 不超过20 | 大于20不超过60 | 超过60 |
19．把1，3，6，10，15，…这些数叫作“三角形数”，这是因为这些数目的点可以排成一个正三角形，则第15个三角形数是（ ）
| A． | 120 | B． | 105 | C． | 153 | D． | 91 |
3．直线l的方程为$|{\begin{array}{l}1&0&2\\ x&2&3\\ y&{-1}&2\end{array}}|=0$，则直线l的一个法向量是（ ）
| A． | （1，2） | B． | （2，1） | C． | （-1，2） | D． | （2，-1） |
13．已知x，y∈R，则“xy＜1是“0＜x＜$\frac{1}{y}$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
如图，在直三棱柱ABC-A1B1C1中，AB=AC=AA1=4，D为BB1上一点，E为AC上一点，且B1D=CE=1，BE=$\sqrt{7}$．