题目内容
18．函数f（x）的定义域为[-1，1]，图象如图1所示：函数g（x）的定义域为[-2，2]，图象如图2所示，方程f[g（x）]=0有m个实数根，方程g[f（x）]=0有n个实数根，则m+n=（ ）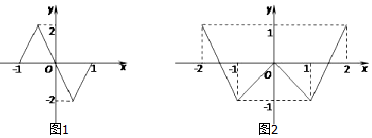
| A． | 14 | B． | 12 | C． | 10 | D． | 8 |
分析 结合函数图象可知，若f（g（x））=0，则g（x）=-1或g（x）=0或g（x）=1；若g（f（x））=0，则f（x）=-1.5或f（x）=1.5或f（x）=0；从而再结合图象求解即可．
解答 解：由图象可知，若f（g（x））=0，则g（x）=-1或g（x）=0或g（x）=1；
由图2知，g（x）=-1时，x=-1或x=1；
g（x）=0时，x的值有3个；g（x）=1时，x=2或x=-2；故m=7；
若g（f（x））=0，则f（x）=-1.5或f（x）=1.5或f（x）=0；
由图1知，f（x）=1.5与f（x）=-1.5各有2个；
f（x）=0时，x=-1，x=1或x=0；故n=7；
故m+n=14；
故选：A．
点评 本题考查了方程的根与函数的图象的关系应用及数形结合的思想应用，属于中档题．
练习册系列答案
相关题目
6．在独立性检验中，统计量Χ2有两个临界值，3.841和6.635，当Χ2＞3.841时，有95%的把握说明两个事件有关，当Χ2＞6.635时，有99%的把握说明两个事件有关，当Χ2＜3.841时，认为两个事件无关，在一项打鼾与患心脏病的调查中，共调出来2000人，经计算Χ2＞20.87，根据这一数据分析，认为打鼾与患心脏病之间（ ）
| A． | 有95%的把握认为两者有关 | B． | 约有95%的打鼾者患心脏病 | ||
| C． | 有99%的把握认为两者有关 | D． | 约有95%的打鼾者患心脏病 |
3．直线l的方程为$|{\begin{array}{l}1&0&2\\ x&2&3\\ y&{-1}&2\end{array}}|=0$，则直线l的一个法向量是（ ）
| A． | （1，2） | B． | （2，1） | C． | （-1，2） | D． | （2，-1） |
10．已知集合A={x|x≤3}，B={x|x2＞4}，则A∩B=（ ）
| A． | {x|-2＜x＜2} | B． | {x|x＜-2或x＞2} | C． | {x|x＜-2或2＜x≤3} | D． | {x|x＜-2或2＜x＜3} |