题目内容
已知点O为△ABC内一点，且
+2
+3
=
，则△AOB，△AOC，△BOC的面积之比等于（ ）
| OA |
| OB |
| OC |
| 0 |
| A、9：4：1 |
| B、1：4：9 |
| C、3：2：1 |
| D、1：2：3 |
考点：平面向量的基本定理及其意义,正弦定理
专题：平面向量及应用
分析：如图所示，延长OB到点E，使得
=2
，分别以
，
为邻边作平行四边形OAFE．则
+2
=
+
=
，由于
+2
+3
=0，可得-
=3
．又
=2
，可得
=2
．于是
=
，得到S△ABC=2S△AOB．同理可得：S△ABC=3S△AOC，S△ABC=6S△BOC．即可得出．
| OE |
| OB |
| OA |
| OE |
| OA |
| OB |
| OA |
| OE |
| OF |
| OA |
| OB |
| OC |
| OF |
| OC |
| AF |
| OB |
| DF |
| OD |
| CO |
| OD |
解答：
解：如图所示，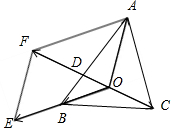
延长OB到点E，使得
=2
，分别以
，
为邻边作平行四边形OAFE．
则
+2
=
+
=
，
∵
+2
+3
=0，∴-
=3
．
又
=2
，可得
=2
．
于是
=
，
∴S△ABC=2S△AOB．
同理可得：S△ABC=3S△AOC，S△ABC=6S△BOC．
∴AOB，△AOC，△BOC的面积比=3：2：1．
故选：C．
延长OB到点E，使得
| OE |
| OB |
| OA |
| OE |
则
| OA |
| OB |
| OA |
| OE |
| OF |
∵
| OA |
| OB |
| OC |
| OF |
| OC |
又
| AF |
| OB |
| DF |
| OD |
于是
| CO |
| OD |
∴S△ABC=2S△AOB．
同理可得：S△ABC=3S△AOC，S△ABC=6S△BOC．
∴AOB，△AOC，△BOC的面积比=3：2：1．
故选：C．
点评：本题考查了向量的平行四边形法则、向量共线定理、三角形的面积计算公式．
练习册系列答案
相关题目
已知函数f（x）=x2-2ax+1对任意x∈（0，1]恒有f（x）≥0成立，则实数a的取值范围是（ ）
| A、[1，+∞） | ||
B、[-
| ||
| C、（-∞，1] | ||
D、（-∞，-
|