题目内容
20.已知函数y=f(x)定义域是[-2,3],则y=f(2x-1)的定义域是( )| A. | $[0,\frac{5}{2}]$ | B. | [-1,4] | C. | $[-\frac{1}{2},2]$ | D. | [-5,5] |
分析 根据复合函数定义域之间的关系即可得到结论.
解答 解:∵函数y=f(x)定义域是[-2,3],
∴由-2≤2x-1≤3,
解得-$\frac{1}{2}$≤x≤2,
即函数的定义域为[-$\frac{1}{2}$,2],
故选:C.
点评 本题主要考查函数定义域的求解,根据复合函数定义域之间的关系解不等式是解决本题的关键,是基础题.

练习册系列答案
相关题目
15.两个变量有线性相关关系且残差的平方和等于0,则( )
| A. | 样本点都在回归直线上 | B. | 样本点都集中在回归直线附近 | ||
| C. | 样本点比较分散 | D. | 不存在规律 |
9.设x0是方程lnx+x=4的解,且x0∈(k,k+1)(k∈Z),求k的值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 0 |
10.若z(1-i)=|1-i|+i(i为虚数单位),则复数z的虚部为( )
| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\sqrt{2}-1$ | C. | 1 | D. | $\frac{{\sqrt{2}+1}}{2}$ |
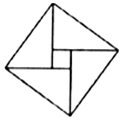 第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.
第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.