题目内容
5.方程x+m=-$\sqrt{4-{x}^{2}}$有且仅有一解,则实数m的取值范围是{-2$\sqrt{2}$}∪(-2,2].分析 由方程根与函数零点的关系,方程x+m=-$\sqrt{4-{x}^{2}}$有且仅有一解,转化为函数y=-$\sqrt{4-{x}^{2}}$与函数y=x+m的图象有且只有一个零点,在同一坐标系中画出两个函数的图象,分析可得答案.
解答 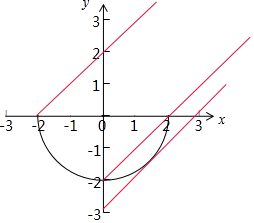 解:方程x+m=-$\sqrt{4-{x}^{2}}$有且仅有一解,
解:方程x+m=-$\sqrt{4-{x}^{2}}$有且仅有一解,
∴函数y=-$\sqrt{4-{x}^{2}}$与函数y=x+m的图象
有且只有一个零点.
如图所示:
当m=-2$\sqrt{2}$时,直线与半圆相切,满足要求,
当m∈(-2,2]时,直线与半圆相交但只有一个交点,
满足要求,
∴实数a的取值范围为{-2$\sqrt{2}$}∪(-2,2].
故答案为:{-2$\sqrt{2}$}∪(-2,2].
点评 本题考查的知识点是函数零点与方程根的关系,其中方程根的个数与函数图象交点个数的转化思想及数形结合思想的引入是解答的关键.

练习册系列答案
相关题目
16.已知命题p:?a∈R,且a>0,a+$\frac{1}{a}$≥2,命题q:?x0∈R,sinx0+cosx0=$\sqrt{3}$,则下列判断正确的是( )
| A. | p是假命题 | B. | q是真命题 | C. | (¬q)是真命题 | D. | (¬p)∧q是真命题 |
13.设函数f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则x•f(x)<0的解集是( )
| A. | {x|-3<x<0或x>3} | B. | {x|x<-3或0<x<3} | C. | {x|x<-3或x>3} | D. | {x|-3<x<0或0<x<3} |
20.已知函数y=f(x)定义域是[-2,3],则y=f(2x-1)的定义域是( )
| A. | $[0,\frac{5}{2}]$ | B. | [-1,4] | C. | $[-\frac{1}{2},2]$ | D. | [-5,5] |
10.设f(x),g(x)是定义域为R的恒大于零的可导函数,且 f'(x)•g(x)-f(x)g'(x)<0,则当b<x<a时有( )
| A. | f(x)•g(x)>f(a)•g(a) | B. | f(x)•g(a)>f(a)•g(x) | C. | f(x)•g(b)>f(b)•g(x) | D. | f(x)•g(x)>f(b)•g(b) |
17.设Sn是等差数列{an}的前n项和,若$\frac{a_7}{a_4}=\frac{7}{13}$,则$\frac{{{S_{13}}}}{S_7}$=( )
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
14.已知函数f(x)=cos(2x+ϕ)(ϕ>0且为常数),下列命题错误的是( )
| A. | 不论ϕ取何值,函数f(x)的周期都是π | |
| B. | 存在常数ϕ,使得函数f(x)是偶函数 | |
| C. | 不论ϕ取何值,函数f(x)在区间[$π-\frac{ϕ}{2},\frac{3π}{2}-\frac{ϕ}{2}$]都是减函数 | |
| D. | 函数f(x)的图象,可由函数y=cos2x的图象向右平移ϕ个单位得到 |
15.已知随机变量X~N(0,σ2),若P(|X|<2)=a,则P(X>2)的值为( )
| A. | $\frac{1-a}{2}$ | B. | $\frac{a}{2}$ | C. | 1-a | D. | $\frac{1+a}{2}$ |
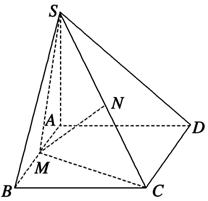 如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.
如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.