题目内容
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．且点A，B的纵坐标分别为| 3 |
| 5 |
| 12 |
| 13 |
（1）若将点B沿单位圆逆时针旋转
| π |
| 2 |
（2）求tan（α+β）的值．
考点：两角和与差的正切函数,任意角的三角函数的定义
专题：三角函数的求值
分析：（1）求出A，B的坐标，将点B沿单位圆逆时针旋转
到达C点，利用两角和与差的三角函数即可求点C的坐标；
（2）求出α、β的正切函数值，利用两角和的正切函数直接求tan（α+β）的值．
| π |
| 2 |
（2）求出α、β的正切函数值，利用两角和的正切函数直接求tan（α+β）的值．
解答：
解：（1）在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．
且点A，B的纵坐标分别为
，
．
∴cosα=
，sinα=
，sinβ=
，cosβ=-
，
将点B沿单位圆逆时针旋转
到达C点，
点C的坐标C（cos（β+
），sin（β+
）），即C（-sinβ，cosβ），
∴C（-
，-
）．
（2）∵cosα=
，sinα=
，sinβ=
，cosβ=-
，∴tanα=
，tanβ=-
．
∴tan（α+β）=
=
=-
．
且点A，B的纵坐标分别为
| 3 |
| 5 |
| 12 |
| 13 |
∴cosα=
| 4 |
| 5 |
| 3 |
| 5 |
| 12 |
| 13 |
| 5 |
| 13 |
将点B沿单位圆逆时针旋转
| π |
| 2 |
点C的坐标C（cos（β+
| π |
| 2 |
| π |
| 2 |
∴C（-
| 12 |
| 13 |
| 5 |
| 13 |
（2）∵cosα=
| 4 |
| 5 |
| 3 |
| 5 |
| 12 |
| 13 |
| 5 |
| 13 |
| 3 |
| 4 |
| 12 |
| 5 |
∴tan（α+β）=
| tanα+tanβ |
| 1-tanαtanβ |
| ||||
1-
|
| 33 |
| 56 |
点评：本题考查任意角的三角函数的定义，两角和的正切函数，基本知识的考查．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知
=a+i（a，b∈R），其中i为虚数单位，则a+b=（ ）
| 1-bi |
| 1+2i |
| A、-4 | B、4 | C、-10 | D、10 |
已知集合 A={0，1，2，3}，集合 B={x∈N||x|≤2}，则A∩B=?（ ）
| A、{ 3 } |
| B、{0，1，2} |
| C、{ 1，2} |
| D、{0，1，2，3} |
设复数z=
（i为虚数单位），z的共轭复数为
，则在复平面内i
对应当点的坐标为（ ）
| 2 |
| -1-i |
. |
| z |
. |
| z |
| A、（1，1） |
| B、（-1，1） |
| C、（1，-1） |
| D、（-1，-1） |
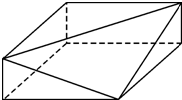某几何体的直观图如图所示，该几何体的主（正）视图和左（侧）视图都正确的是（ ）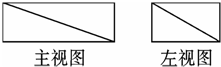
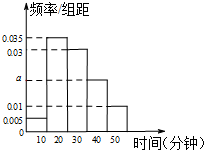某学校为调查高一新生上学路程所需要的时间（单位：分钟），从高一年级新生中随机抽取100名新生按上学所需时间分组：第1组（0，10]，第2组（10，20]，第3组（20，30]，第4组（30，40]，第5组（40，50]，得到的频率分布直方图如图所示．
在△ABC中，角A，B，C所对的边分别是a，b，c，cosC=-