题目内容
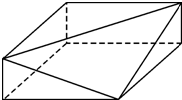某几何体的直观图如图所示，该几何体的主（正）视图和左（侧）视图都正确的是（ ）A、 |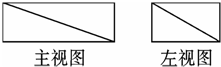
B、 |
C、 |
D、 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体是长方体削去一个三棱锥，根据正视图、左视图的定义及看到的棱画实线，看不到的棱画虚线，可得几何体的正视图与左视图．
解答：
解：由直观图知：几何体是长方体削去一个三棱锥，
∴其正视图是矩形，且矩形内有一条对角线是实线；
左视图是矩形，且矩形内有一条对角线是虚线．
故选：B．
∴其正视图是矩形，且矩形内有一条对角线是实线；
左视图是矩形，且矩形内有一条对角线是虚线．
故选：B．
点评：本题考查了几何体的直观图判断其三视图，熟练掌握正视图、左视图的定义是关键．
练习册系列答案
相关题目
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，则f（0）的值为（ ）
| A、1 | ||
| B、0 | ||
C、
| ||
D、
|
已知函数f（x）=-
x3+2ax2+3x（a＞0）的导数f′（x）的最大值为5，则在函数f（x）图象上的点（1，f（1））处的切线方程是（ ）
| 2 |
| 3 |
| A、3x-15y+4=0 |
| B、15x-3y-2=0 |
| C、15x-3y+2=0 |
| D、3x-y+1=0 |
实数x，y满足条件
，则22x-y的最小值为（ ）
|
A、
| ||
B、
| ||
| C、1 | ||
| D、4 |
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．且点A，B的纵坐标分别为