题目内容
 在△ABC中,角A,B,C所对的边分别是a,b,c,cosC=-
在△ABC中,角A,B,C所对的边分别是a,b,c,cosC=-
| ||
| 4 |
(1)若c=
| 2 |
(2)当b=2,sinB=
| ||
| 8 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)利用余弦定理表示出cosC,将c=
a代入根据cosC的值小于0,即可判断出a与b的大小;
(2)由cosC的值求出sinC的值,得到sinC=2sinB,利用正弦定理化简c=2b,根据b的值求出c的值,根据sinB的值求出cosB的值,利用余弦定理表示出cosC,将b与c的值代入求出a的值,再利用余弦定理即可求出CD的值.
| 2 |
(2)由cosC的值求出sinC的值,得到sinC=2sinB,利用正弦定理化简c=2b,根据b的值求出c的值,根据sinB的值求出cosB的值,利用余弦定理表示出cosC,将b与c的值代入求出a的值,再利用余弦定理即可求出CD的值.
解答:
 解:(1)∵c=
解:(1)∵c=
a,
∴cosC=
=
=
=-
<0,即b2-a2=(b+a)(b-a)<0,
∴b-a<0,即a>b;
(2)∵cosC=-
,sinB=
,
∴sinC=
=
=2×
=2sinB,
∵b=2,
∴利用正弦定理化简得:c=2b=4,
∵sinB=
,
∴cosB=
=
,
∵cosC=
=-
,
解得:a=
,
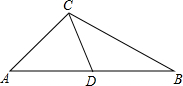
在△BCD中,BC=a=
,BD=
AB=
c=2,cosB=
,
利用余弦定理得:CD2=(
)2+22-2×
×2×
=6+4-9=1,
解得:CD=1.
 解:(1)∵c=
解:(1)∵c=| 2 |
∴cosC=
| a2+b2-c2 |
| 2ab |
| a2+b2-2a2 |
| 2ab |
| b2-a2 |
| 2ab |
| ||
| 4 |
∴b-a<0,即a>b;
(2)∵cosC=-
| ||
| 4 |
| ||
| 8 |
∴sinC=
| 1-cos2C |
| ||
| 4 |
| ||
| 8 |
∵b=2,
∴利用正弦定理化简得:c=2b=4,
∵sinB=
| ||
| 8 |
∴cosB=
| 1-sin2B |
3
| ||
| 8 |
∵cosC=
| a2+4-16 |
| 4a |
| ||
| 4 |
解得:a=
| 6 |
在△BCD中,BC=a=
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 8 |
利用余弦定理得:CD2=(
| 6 |
| 6 |
3
| ||
| 8 |
解得:CD=1.
点评:此题考查了正弦、余弦定理,以及同角三角函数间的基本关系,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.且点A,B的纵坐标分别为
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.且点A,B的纵坐标分别为 如图几何体中,四边形ABCD为矩形,AB=3BC=6,BF=CF=AE=DE=2,EF=4,EF∥AB,G为FC的中点,M为线段CD上的一点,且CM=2.
如图几何体中,四边形ABCD为矩形,AB=3BC=6,BF=CF=AE=DE=2,EF=4,EF∥AB,G为FC的中点,M为线段CD上的一点,且CM=2.