Question

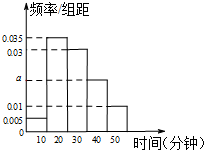某学校为调查高一新生上学路程所需要的时间（单位：分钟），从高一年级新生中随机抽取100名新生按上学所需时间分组：第1组（0，10]，第2组（10，20]，第3组（20，30]，第4组（30，40]，第5组（40，50]，得到的频率分布直方图如图所示．
（Ⅰ）根据图中数据求a的值；
（Ⅱ）若从第3，4，5组中用分层抽样的方法抽取6名新生参与交通安全问卷调查，应从第3，4，5组各抽取多少名新生？
（Ⅲ）在（Ⅱ）的条件下，该校决定从这6名新生中随机抽取2名新生参加交通安全宣传活动，求第4组至少有一名志愿者被抽中的概率．

Answer 1

考点：古典概型及其概率计算公式,频率分布直方图

专题：概率与统计

分析：（I）由各组的累积频率为1，构造关于a的方程，解方程可得a的值；
（Ⅱ）先计算各组学生的人数，进而求出抽样比，就可得到应从第3，4，5组各抽取多少名新生；
（Ⅲ）先计算从6名新生中抽取2名新生所有的情况总数，再求出第4组至少有一名志愿者被抽中的情况数，代入古典概型概率计算公式，可得答案．

解答： 解：（Ⅰ）∵（0.005+0.01+a+0.03+0.035）×10=1，…（1分）
所以a=0.02．…（2分）
（Ⅱ）依题意可知，
第3组的人数为0.3×100=30，
第4组的人数为0.2×100=20，
第5组的人数为0.1×100=10．
所以3、4、5组人数共有60．…（3分）
所以利用分层抽样的方法在60名学生中抽取6名新生，分层抽样的抽样比为

6

60

=

1

10

．…（4分）
所以在第3组抽取的人数为3人，
在第4组抽取的人数为2人，
在第5组抽取的人数为1人，…（7分）
（Ⅲ）记第3组的3名新生为A，B，C，第4组的2名新生为a，b，第5组的1名新生为1．
则从6名新生中抽取2名新生，共有：
（A，B），（A，C），（A，a），（A，b），（A，1），
（B，C），（B，a），（B，b），（B，1），（C，a），
（C，b），（C，1），（a，b），（a，1），（b，1），共有15种．…（9分）
其中第4组的2名新生a，b至少有一名新生被抽中的有：
（A，a），（A，b），（B，a），（B，b），（C，a），
（C，b），（a，b），（a，1），（b，1），共有9种，…（11分）
则第4组至少有一名新生被抽中的概率P=

9

15

=

3

5

                …（13分）

点评：本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．