题目内容
设sin2α=-sinα,α∈(
,π),则tanα的值是 .
| π |
| 2 |
考点:二倍角的余弦,同角三角函数间的基本关系
专题:三角函数的求值
分析:依题意,利用二倍角的正弦可得cosα=-
,又α∈(
,π),可求得α的值,继而可得tanα的值.
| 1 |
| 2 |
| π |
| 2 |
解答:
解:∵sin2α=2sinαcosα=-sinα,
∴cosα=-
,又α∈(
,π),
∴α=
,
∴tanα=-
.
故答案为:-
.
∴cosα=-
| 1 |
| 2 |
| π |
| 2 |
∴α=
| 2π |
| 3 |
∴tanα=-
| 3 |
故答案为:-
| 3 |
点评:本题考查同角三角函数间的基本关系与二倍角的正弦,属于基础题.

练习册系列答案
相关题目
设a=log0.34,b=log0.30.2,c=(
)π( )
| 1 |
| e |
| A、a>b>c |
| B、b>c>a |
| C、b>a>c |
| D、c>b>a |
设函数D(x)=
,关于函数D(x)有以下四个结论:
①D(x)值域为[0,1];②D(x)是周期函数;③D(x)是单调函数;④D(x)是偶函数;
其中正确的结论个数为( )
|
①D(x)值域为[0,1];②D(x)是周期函数;③D(x)是单调函数;④D(x)是偶函数;
其中正确的结论个数为( )
| A、0 | B、1 | C、2 | D、3 |
已知函数f(x)是定义在(-6,6)上的偶函数,f(x)在[0,6]上是单调函数,且f(-2)≤f(1),f(-2)=25,那么下列肯定不正确的是( )
| A、f(1)≥25 |
| B、f(2)=25 |
| C、f(1)<25 |
| D、f(1)>25 |
设函数f(x)(x∈R)满足f(x+2)=f(x)+2.当0≤x<2时,f(x)=1,则f(2014)=( )
| A、2013 | B、2014 |
| C、2015 | D、2016 |
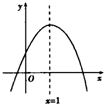 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论: