题目内容

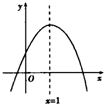已知二次函数y=ax2+bx+c的图象如图所示，对称轴是x=1．给出下列四个结论：
①ac＞0；
②b＞0；
③b2-4ac＞0；
④2a+b=0．
其中正确结论的个数是（　　）
A、0B、1C、2D、3
考点：二次函数的性质
专题：函数的性质及应用
分析：由二次函数y=ax2+bx+c的图象结合开口方向与y轴交点坐标及对称轴是x=1逐一分析四个结论的真假，可得答案．
解答： 解：∵图象与x轴有两个交点，则方程有两个不相等的实数根，b2-4ac＞0，故③正确；
∵函数图象开口向下，故a＜0，有-
b
2a
＞0，则b＞0，故②正确；
对称轴为x=1=-
b
2a
，则2a+b=0，故④正确；
又∵c＞0，故ac＜0，故①错误；
故选：D
点评：解答此题要注意函数与方程的关系，关键是掌握二次函数y=ax2+bx+c系数符号的确定．
练习册系列答案
相关题目
已知f（x）=x3+ax2+bx+c，当x=1时f（x）的极大值为7，当x=3 时，f（x）有极小值，
（1）求a，b，c的值．
（2）函数f（x）的极值．
在实数集R中定义一种运算“*”，?a，b∈R，a*b为唯一确定的实数，且具有性质：
（1）对任意a∈R，a*0=a；
（2）对任意a，b∈R，a*b=ab+（a*0）+（b*0）．
关于函数f（x）=（ex）•
1
ex
的性质，有如下说法：①函数f（x）的最小值为3；②函数f（x）为偶函数；③函数f（x）的单调递增区间为（-∞，0]．
其中所有正确说法的个数为（　　）
A、0B、1C、2D、3
如果函数y=logax在区间[2，+∞﹚上恒有y＞1，求实数a的取值范围．
若函数y=sin（wx+Φ）（w＞0）的部分图象如图，则w=（　　）
A、1B、2C、3D、4
设sin2α=-sinα，α∈（
π
2
，π），则tanα的值是
 
．
已知圆C的圆心在坐标原点O，且与直线l1：x-y-2
2
=0相切．
（1）求直线l2：4x-3y+5=0被圆C所截得的弦AB的长；
（2）若与直线l1垂直的直线与圆C交于不同的两点P，Q，且以PQ为直径的圆过原点，求直线的纵截距；
（3）过点G（1，3）作两条与圆C相切的直线，切点分别为M，N，求直线MN的方程．
已知点M是y=
1
4
x2上一点，F为抛物线的焦点，A在C：（x-1）2+（y-4）2=1上，则|MA|+|MF|的最小值为
 
．
在△ABC中，角A，B，C的对边分别是a，b，c，设S为△ABC的面积，且S=
3
4
（a2+b2-c2）．
（1）求角C的大小；
（2）当cosA+cosB取得最大值时，判断△ABC的形状．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网