题目内容
18．已知扇形的弧长为π，面积为2π，则这个扇形的圆心角的弧度数为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | 2 | D． | 4 |
分析 首先根据扇形的面积求出半径，再由弧长公式得出结果．
解答 解：根据扇形的面积公式S=$\frac{1}{2}$lr，可得：2π=$\frac{1}{2}$×πr，
解得：r=4，
再根据弧长公式l=4α，
解得扇形的圆心角的弧度数是$\frac{π}{4}$
故选：A．
点评 此题主要是利用扇形的面积公式先求出扇形的半径，再利用弧长公式求出圆心角，属于基础题．
练习册系列答案
相关题目
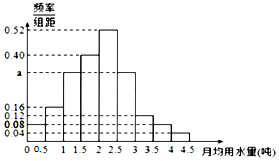我国是世界上严重缺水的国家，某市政府为了鼓励全市30万居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超过x的部分按议价收费，并希望约80%的居民每月的用水量不超过标准x（吨）．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），[4，4.5）分成9组，制成了如图所示的频率分布直方图．
13．若以等边三角形ABC的顶点A，B为焦点的双曲线恰好过BC的中点，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\sqrt{3}+1$ |
交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T，其范围分为五个级别，T∈[0，2）畅通；T∈[2，4）基本畅通； T∈[4，6）轻度拥堵；T∈[6，8）中度拥堵；T∈[8，10]严重拥堵．早高峰时段（T≥3），从某市交通指挥中心随机选取了三环以内的50个交通路段，依据其交通指数数据绘制的频率分布直方图如图．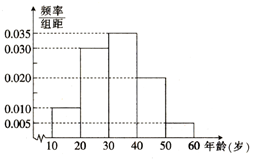
随着医院对看病挂号的改革，网上预约成为了当前最热门的就诊方式，这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题；某医院研究人员对其所在地区年龄在10～60岁间的n位市民对网上预约挂号的了解情况作出调查，并将被调查的人员的年龄情况绘制成频率分布直方图，如右图所示．