题目内容
7.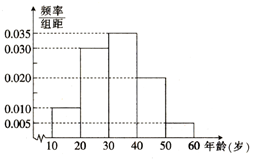 随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示.
随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示.(1)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(2)若按分层抽样的方法从年龄在[20,30)以内及[40,50)以内的市民中随机抽取10人,再从这10人中随机抽取3人进行调研,记随机抽的3人中,年龄在[40,50)以内的人数为X,求X的分布列以及数学期望.
分析 (1)由频率分布列求出被调查的人员年龄在20~30岁间的市民的频率,由此求出n,再求出被调查人员的年龄在40岁以上(含40岁)的市民的频率,从而能求出被调查人员的年龄在40岁以上(含40岁)的市民人数.
(2)年龄在[20,30)内的市民有300人,年龄在[40,50)内的市民有200人,按分层抽样的方法从年龄在[20,30)以内及[40,50)以内的市民中随机抽取10人,年龄在[20,30)内的市民抽中6人,年龄在[40,50)内的市民抽中4人,从而X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及数学期望.
解答 解:(1)由频率分布列知被调查的人员年龄在20~30岁间的市民的频率为0.030×10=0.3,
∵被调查的人员年龄在20~30岁间的市民有300人,
∴n=$\frac{300}{0.3}$=1000,
∵被调查人员的年龄在40岁以上(含40岁)的市民的频率为(0.020+0.005)×10=0.25,
∴被调查人员的年龄在40岁以上(含40岁)的市民人数为:0.25×1000=250人.
(2)年龄在[20,30)内的市民有:0.030×1000=300人,
年龄在[40,50)内的市民有:0.020×1000=200人,
按分层抽样的方法从年龄在[20,30)以内及[40,50)以内的市民中随机抽取10人,
年龄在[20,30)内的市民抽中300×$\frac{10}{300+200}$=6人,
年龄在[40,50)内的市民抽中:200×$\frac{10}{300+200}$=4人,
再从这10人中随机抽取3人进行调研,记随机抽的3人中,年龄在[40,50)以内的人数为X,
则X的可能取值为0,1,2,3,
P(X=0)=$\frac{{C}_{6}^{3}}{{C}_{10}^{3}}$=$\frac{1}{6}$,
P(X=1)=$\frac{{C}_{6}^{2}{C}_{4}^{1}}{{C}_{10}^{3}}$=$\frac{1}{2}$,
P(X=2)=$\frac{{C}_{6}^{1}{C}_{4}^{2}}{{C}_{10}^{3}}$=$\frac{3}{10}$,
P(X=3)=$\frac{{C}_{4}^{3}}{{C}_{10}^{3}}$=$\frac{1}{30}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{2}$ | $\frac{3}{10}$ | $\frac{1}{30}$ |
点评 本题考查频率分布直方图、分层抽样的应用,考查离散型随机变量的分布列、数学期望的求法,是中档题,解题时要认真审题,注意频率分布直方图的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | 2 | D. | 4 |
| A. | 命题:“若x≠2,则x2-5x+6≠0”的逆否命题是“若x2-5x+6=0,则x=2” | |
| B. | “x<1”是“x2-3x+2>0”的充分不必要条件 | |
| C. | 若命题“p:?x∈R,x2+x+1≠0”,则“¬p:?x0∈R,x02+x0+1=0” | |
| D. | 若“p∨q”为真命题,则p,q均为真命题 |
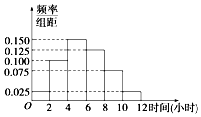 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12]
①估计该校学生每周平均体育运动时间超过4小时的概率P;
②假设该校每个学生每周平均体育运动时间超过4小时的概率都为P,试求从中任选三人至少有一人每周平均体育运动时间超过4小时的概率
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
| A. | “x2=1”是“x=1”的充分不必要条件 | |
| B. | “x=2时,x2-3x+2=0”的否命题为真命题 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |