题目内容

8．在侧棱长为$2\sqrt{3}$的正三棱锥S-ABC中，∠ASB=∠BSC=∠CSA=40°，过A作截面AMN，交SB于M，交SC于N，则截面AMN周长的最小值为6．

分析 把三棱锥的侧面沿其中一条侧棱SA展开成平面，则截面AMN周长最小值求解三角形边长即可．

解答 解：将三棱锥S-ABC侧面沿SA剪开展成如下平面图形．
观察图形知：

当A，M，N三点共线时，△AMN的周长最小，
此时，△AMN的周长=AN+MN+AM=2•ASsin60°=2×2$\sqrt{3}$sin60°=6．
故答案为：6．

点评 本题考查三角形周长的最小值的求法，是中档题，解题的关键是把三棱锥展成平面图形，合理地化空间问题为平面问题．

练习册系列答案
相关题目
18．若奇函数f（x）定义域为R，f（x+2）=-f（x）且f（-1）=6，则f（2017）=-6．
19．设全集U={1，2，3，4，5，6，7，8}，集合A={1，2，3，5}，B={2，4，6}，则B∩∁UA=（　　）
A．{2}B．{4，6}C．{1，3，5}D．{4，6，7，8}
16．设函数$f（x）=\left\{\begin{array}{l}\int_1^e{\frac{1}{t}dt，x＞\sqrt{2}}\\ \frac{1}{3}，x≤\sqrt{2}\end{array}\right.$，若$f（{x_0}）＞\frac{1}{2}$，则x0的取值范围为x0＞$\sqrt{2}$．
3．已知函数f（x）=ax2+bx+clnx（a，b，c∈R）．
（1）当a=-1，b=2，c=0时，求曲线y=f（x）在点（2，0）处的切线方程；
（2）当a=1，b=0时，求函数f（x）的极值；
（3）当b=-2a，c=1时，是否存在实数a，使得0＜x≤2时，函数y=f（x）图象上的点都在$\left\{\begin{array}{l}0＜x≤2\\ x-y-1≥0\end{array}\right.$所表示的平面区域内（含边界）？若存在，求出a的取值范围；若不存在，请说明理由．
13．定义在R上的单调函数f（x）满足：f（x+y）=f（x）+f（y），若F（x）=f（asinx）+f（sinx+cos2x-3）在（0，π）上有零点，则a的取值范围是[2，+∞）．
20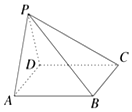．如图，在四棱锥P-ABCD中，侧面PAD是边长为4的正三角形，底面ABCD为正方形，侧面PAD⊥底面ABCD，M为底面ABCD内的一个动点，且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$，则点M到直线AB的最短距离为（　　）
A．$\sqrt{5}$B．$4-\sqrt{5}$C．$3-\sqrt{5}$D．$4-2\sqrt{2}$
17．已知菱形ABCD的边长为2，∠ABC=60°，则$\overrightarrow{BD}$•$\overrightarrow{CD}$=6．
18．已知扇形的弧长为π，面积为2π，则这个扇形的圆心角的弧度数为（　　）
A．$\frac{π}{4}$B．$\frac{π}{2}$C．2D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网