题目内容
10. 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.(Ⅰ)这50个路段为中度拥堵的有多少个?
(Ⅱ)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
分析 (Ⅰ)由频率分布直方图先求出这50个路段为中度拥堵的频率,由此能求出求出这50个路段为中度拥堵的个数.
(Ⅱ)设事件A为“一个路段严重拥堵”,则P(A)=0.1,事件B“至少一个路段严重拥堵”,P($\overline{B}$)=(1-P(A))3,由此能求出早高峰三环以内的三个路段至少有一个是严重拥堵的概率.
解答 解:(Ⅰ)由频率分布直方图得:
这50个路段为中度拥堵的有:(0.2+0.16)×1×50=18个.
(Ⅱ)设事件A为“一个路段严重拥堵”,则P(A)=0.1,
事件B“至少一个路段严重拥堵”,
则P($\overline{B}$)=(1-P(A))3=0.729,
∴早高峰三环以内的三个路段至少有一个是严重拥堵的概率:
P(B)=1-P($\overline{B}$)=1-0.729=0.271.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
20.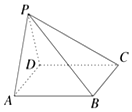 如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )
如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )
 如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )
如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$,则点M到直线AB的最短距离为( )| A. | $\sqrt{5}$ | B. | $4-\sqrt{5}$ | C. | $3-\sqrt{5}$ | D. | $4-2\sqrt{2}$ |
1.在公差为d,各项均为正整数的等差数列{an}中,若a1=1,an=51,则n+d的最小值为( )
| A. | 14 | B. | 16 | C. | 18 | D. | 10 |
18.已知扇形的弧长为π,面积为2π,则这个扇形的圆心角的弧度数为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | 2 | D. | 4 |
2.下列选项错误的是( )
| A. | 命题:“若x≠2,则x2-5x+6≠0”的逆否命题是“若x2-5x+6=0,则x=2” | |
| B. | “x<1”是“x2-3x+2>0”的充分不必要条件 | |
| C. | 若命题“p:?x∈R,x2+x+1≠0”,则“¬p:?x0∈R,x02+x0+1=0” | |
| D. | 若“p∨q”为真命题,则p,q均为真命题 |
19. 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
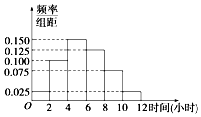
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12]
①估计该校学生每周平均体育运动时间超过4小时的概率P;
②假设该校每个学生每周平均体育运动时间超过4小时的概率都为P,试求从中任选三人至少有一人每周平均体育运动时间超过4小时的概率
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$.
 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12]
①估计该校学生每周平均体育运动时间超过4小时的概率P;
②假设该校每个学生每周平均体育运动时间超过4小时的概率都为P,试求从中任选三人至少有一人每周平均体育运动时间超过4小时的概率
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
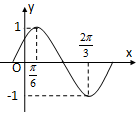 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.