题目内容
13.若以等边三角形ABC的顶点A,B为焦点的双曲线恰好过BC的中点,则双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{3}+1$ |
分析 根据正△ABC的顶点A、B为焦点的双曲线恰好平分边AC、BC,利用正三角形的性质,结合双曲线的定义,即可求出双曲线的离心率.
解答 解:由题意,设BC中点为D,则AB=2c,
∵正△ABC的顶点A、B为焦点的双曲线恰好平分边AC、BC,
∴BD=c,AD=$\sqrt{3}$c,
∴2a=($\sqrt{3}$-1)c,
∴e=$\frac{c}{a}$=$\sqrt{3}$+1,
故选:D.
点评 本题考查双曲线的几何性质,考查正三角形的性质,正确理解双曲线的定义是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.在公差为d,各项均为正整数的等差数列{an}中,若a1=1,an=51,则n+d的最小值为( )
| A. | 14 | B. | 16 | C. | 18 | D. | 10 |
8.在△ABC中,角A,B,C的对边分别为a,b,c,∠A,∠B,∠C的大小成等差数列,且a=1,$b=\sqrt{3}$.则∠A的大小为( )
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$或$\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
18.已知扇形的弧长为π,面积为2π,则这个扇形的圆心角的弧度数为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | 2 | D. | 4 |
2.下列选项错误的是( )
| A. | 命题:“若x≠2,则x2-5x+6≠0”的逆否命题是“若x2-5x+6=0,则x=2” | |
| B. | “x<1”是“x2-3x+2>0”的充分不必要条件 | |
| C. | 若命题“p:?x∈R,x2+x+1≠0”,则“¬p:?x0∈R,x02+x0+1=0” | |
| D. | 若“p∨q”为真命题,则p,q均为真命题 |
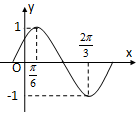 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.