题目内容
设A为双曲线
-
=1右支上一点，F为该双曲线的右焦点，连AF交双曲线于B，过B作直线BC垂直于双曲线的右准线，垂足为C，求证：直线AC恒过定点．
| x2 |
| 16 |
| y2 |
| 9 |
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：由于研究直线恒过定点，求出AC的方程，令y=0，求出x可得（x与直线AB斜率k无关），可证直线AC恒过定点就可解决．
解答：
证明：由双曲线的方程可得a=4，b=3，c=5，右焦点 F（5，0 ），右准线为x=
，
设直线AB：x=my+5，与双曲线方程
-
=1联立，可得（9m2-16）y2+90my+81=0，
设A（x1，y1），B（x2，y2），则y1+y2=-
，y1y2=
用两点式求出直线AC的方程，y-y2=
（x-
）
令y=0，可得x=
+
=
=
=
，
∴直线AC过定点（
，0）．
| 16 |
| 5 |
设直线AB：x=my+5，与双曲线方程
| x2 |
| 16 |
| y2 |
| 9 |
设A（x1，y1），B（x2，y2），则y1+y2=-
| 90m |
| 9m2-16 |
| 81 |
| 9m2-16 |
用两点式求出直线AC的方程，y-y2=
| y2-y1 | ||
|
| 16 |
| 5 |
令y=0，可得x=
-
| ||
| y2-y1 |
| 16 |
| 5 |
-
| ||
| y2-y1 |
=
| ||||
|
| 41 |
| 10 |
∴直线AC过定点（
| 41 |
| 10 |
点评：本题考查直线恒过定点，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知集合A={x|y=
-
}，则B={x|x≤6}，则A∩B等于（ ）
| x-2 |
| 8-x |
| A、[2，6） |
| B、[2，6] |
| C、[2，8] |
| D、（-∞，6] |
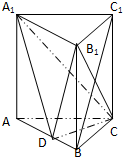已知三棱柱ABC-A1B1C1中，侧棱垂直于底面，AC=BC，点D是AB的中点．