题目内容
若点T(x0,y0)是抛物线:y2=4x上的动点,则圆:(x-x0)2+(y-y0)2=(1+x0)2恒过定点是 .
考点:圆与圆锥曲线的综合
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,y02=4x0,化简(x-x0)2+(y-y0)2=(1+x0)2为
y02(1-x)-2y0y+x2+y2-1=0,从而得x=1,y=0.
| 1 |
| 2 |
解答:
解:由题意,y02=4x0,
∵(x-x0)2+(y-y0)2=(1+x0)2,
∴x2-2x0x+x02+y2-2y0y+y02=1+2x0+x02,
∴x2-2x0x+y2-2y0y+y02=1+2x0,
∴x2-
y02x+y2-2y0y+y02=1+
y02,
∴
y02(1-x)-2y0y+x2+y2-1=0,
则令1-x=0,y=0,x2+y2-1=0,
解得,x=1,y=0.
故答案为:(1,0).
∵(x-x0)2+(y-y0)2=(1+x0)2,
∴x2-2x0x+x02+y2-2y0y+y02=1+2x0+x02,
∴x2-2x0x+y2-2y0y+y02=1+2x0,
∴x2-
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
则令1-x=0,y=0,x2+y2-1=0,
解得,x=1,y=0.
故答案为:(1,0).
点评:本题考查了学生的化简运算能力及恒成立问题的处理方法,属于中档题.

练习册系列答案
相关题目
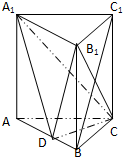 已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.
已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.