题目内容

方程f（x）=x的根称为f（x）的不动点，若函数f（x）=
x
a(x+2)
有唯一不动点，且x1=1000，xn+1=
1
f(
1
xn
)
（n∈N*），则x2013=（　　）
A、2006B、2008
C、2012D、2013
考点：函数的零点
专题：计算题,函数的性质及应用,等差数列与等比数列
分析：由题意，f（x）-x=
x
a(x+2)
-x=0有且只有一个解，从而解a；从而可得{xn}是以
1
2
为公差的等差数列，从而求解．
解答： 解：由题意，f（x）-x=
x
a(x+2)
-x=0有且只有一个解，
故a=
1
2
；
则xn+1=
1
f(
1
xn
)
=1÷
1
xn
1
2
(
1
xn
+2)
=
1+2xn
2
=
1
2
+xn；
故{xn}是以
1
2
为公差的等差数列，
故x2013=x1+（2012）×
1
2

=1000+1006=2006；
故选A．
点评：本题考查了函数的零点的求法及等差数列的应用，属于基础题．
练习册系列答案
相关题目
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两条渐近线与抛物线y2=2px（p＞0）的准线分别交于A、B两点，O为坐标原点，若双曲线的离心率为2，△AOB的面积为
3
，则该抛物线的标准方程是
 
．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）过点A（1，
3
2
），它的一个焦点是F（-1，0）．
（1）求椭圆的方程；
（2）P，Q是椭圆C上的两个动点，如果直线AP的倾斜角与AQ的倾斜角互补，证明：直线PQ定向（即该直线的斜率为定值）．
双曲线上右支上存在点P，使得右焦点F关于直线OP的对称点在y轴上（O为坐标原点），则双曲线离心率的取值范围为（　　）
A、(
2
，
3
)
B、(
2
，+∞)
C、(1，
2
)
D、(
3
，+∞)
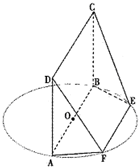AB为圆O的直径，点E、F在圆上，AB∥EF，矩形ABCD所在平面与圆O所在平面互相垂直，已知AB=2，BC=EF=1．
（Ⅰ）求证：BF⊥平面DAF；
（Ⅱ）求多面体ABCDFE的体积．
在极坐标系中，点（3，
π
2
）到直线ρsin（θ-
π
4
）=2
2
的距离为
 
．
已知函数f（x）=
2x-4(x≤1)
x2-2x-1(x＞1)
则函数y=f（x）-log2x的零点的个数是（　　）
A、1B、2C、3D、4
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞0，b＞0）的离心率为
2
2
，其左右焦点分别为F1，F2，点P（x0，y0）是圆x2+y2=
7
4
上一点，且
PF1
•
PF2
=
3
4
．
（1）求椭圆C的方程；
（2）设不垂直x轴的直N线l：y=kx+m与椭圆C交于M，N两点，直线F2M与F2N倾斜角分别为α，β，且α+β=π．证明直线l过定点，并求出定点坐标．
若x1，x2是函数f（x）=x2+mx-2（m∈R）的两个零点，且x1＜x2，则x2-x1的最小值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网