题目内容
已知椭圆
+
=1(a>b>0)过点A(1,
),它的一个焦点是F(-1,0).
(1)求椭圆的方程;
(2)P,Q是椭圆C上的两个动点,如果直线AP的倾斜角与AQ的倾斜角互补,证明:直线PQ定向(即该直线的斜率为定值).
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
(1)求椭圆的方程;
(2)P,Q是椭圆C上的两个动点,如果直线AP的倾斜角与AQ的倾斜角互补,证明:直线PQ定向(即该直线的斜率为定值).
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)方程组
得出椭圆的方程.
(2)化简得出(3+4k2)x2-8k(k-
)x-4k2-12k-3=0,韦达定理求解即可.
|
(2)化简得出(3+4k2)x2-8k(k-
| 3 |
| 2 |
解答:
解:(1)∵椭圆
+
=1(a>b>0)过点A(1,
),它的一个焦点是F(-1,0).
∴
,
a2=4,b2=3,
椭圆方程
+
=1.
(2)由题意可知直线AP,AQ斜率均存在,且互为相反数,
设直线AP的方程为:y-
=k(x-1)代入椭圆方程
+
=1.化简得
(3+4k2)x2-8k(k-
)x-4k2-12k-3=0,其一根为1,
由韦达定理可得:xp=
,yp=
+
用-k代入xQ=
,yp=
+
,
kPQ=
.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
∴
|
a2=4,b2=3,
椭圆方程
| x2 |
| 4 |
| y2 |
| 3 |
(2)由题意可知直线AP,AQ斜率均存在,且互为相反数,
设直线AP的方程为:y-
| 3 |
| 2 |
| x2 |
| 4 |
| y2 |
| 3 |
(3+4k2)x2-8k(k-
| 3 |
| 2 |
由韦达定理可得:xp=
| 4k2-12k-3 |
| 3+4k2 |
| -12k2+6k |
| 3+4k2 |
| 3 |
| 2 |
用-k代入xQ=
| 4k2+12k-3 |
| 3+4k2 |
| -12k2+6k |
| 3+4k2 |
| 3 |
| 2 |
kPQ=
| 1 |
| 2 |
点评:本题考查了椭圆的简单几何性质,直线与椭圆的位置关系,方程的思想,属于难题,关键是仔细计算,求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
设F1,F2为双曲线C:
-
=1(a>0,b>0)的左、右焦点,且直线y=2x为双曲线C的一条渐近线,点P为C上一点,如果|PF1|-|PF2|=4,那么双曲线C的方程为 ;离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
若a是从集合{1,2,3,4}中随机抽取的一个数,b是从集合{1,2,3}中抽取的一个数,则关于x的方程x2+2ax+b2=0有实数根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某电商在“双十一”期间用电子支付系统进行商品买卖,全部商品共有n类(n∈N*),分别编号为1,2,…,n,买家共有m名(m∈N*,m<n),分别编号为1,2,…,m.若aij=
1≤i≤m,1≤j≤n,则同时购买第1类和第2类商品的人数是( )
|
| A、a11+a12+…+a1m+a21+a22+…+a2m |
| B、a11+a21+…+am1+a12+a22+…+am2 |
| C、a11a12+a21a22+…+am1am2 |
| D、a11a21+a12a22+…+a1ma2m |
方程f(x)=x的根称为f(x)的不动点,若函数f(x)=
有唯一不动点,且x1=1000,xn+1=
(n∈N*),则x2013=( )
| x |
| a(x+2) |
| 1 | ||
f(
|
| A、2006 | B、2008 |
| C、2012 | D、2013 |
定义在R上的函数f(x)满足f(1)=l,且对一切x∈R都有f′(x)<4,则不等式f(x)>4x-3的解集为( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
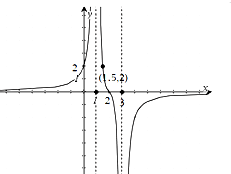 已知函数y=f(x)的图象(如图所示)过点(0,2)、(1.5,2)和点(2,0),且函数图象关于点(2,0)对称;直线x=1和x=3及y=0是它的渐近线.现要求根据给出的函数图象研究函数g(x)=
已知函数y=f(x)的图象(如图所示)过点(0,2)、(1.5,2)和点(2,0),且函数图象关于点(2,0)对称;直线x=1和x=3及y=0是它的渐近线.现要求根据给出的函数图象研究函数g(x)=