题目内容
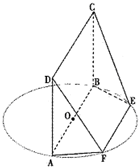 AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.
AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.(Ⅰ)求证:BF⊥平面DAF;
(Ⅱ)求多面体ABCDFE的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)由已知得AD⊥平面ABEF,AD⊥BF,AF⊥BF,由此能证明BF⊥平面DAF.
(Ⅱ)作FA′⊥AB,EB′⊥AB,FD′⊥CD,EC′⊥CD,A′,B′,C′,D′为垂足,多面体ABCDFE的体积V=VFA′D′-EB′C′+2VF-AA′D′D,由此能求出结果.
(Ⅱ)作FA′⊥AB,EB′⊥AB,FD′⊥CD,EC′⊥CD,A′,B′,C′,D′为垂足,多面体ABCDFE的体积V=VFA′D′-EB′C′+2VF-AA′D′D,由此能求出结果.
解答:
(本题满分12分)
(Ⅰ)证明:因为平面ABCD⊥平面ABEF,AD⊥AB,
∴AD⊥平面ABEF,∴AD⊥BF;
又∵AB为圆O的直径,∴AF⊥BF,
AF∩AD=A,
∴BF⊥平面DAF.…(6分)
(Ⅱ)解:作FA′⊥AB,EB′⊥AB,FD′⊥CD,EC′⊥CD,
A′,B′,C′,D′为垂足,
则多面体ABCDFE的体积V=VFA′D′-EB′C′+2VF-AA′D′D
=
×
×1×1+2×
×
×1×
=
.…(12分)
(Ⅰ)证明:因为平面ABCD⊥平面ABEF,AD⊥AB,

∴AD⊥平面ABEF,∴AD⊥BF;
又∵AB为圆O的直径,∴AF⊥BF,
AF∩AD=A,
∴BF⊥平面DAF.…(6分)
(Ⅱ)解:作FA′⊥AB,EB′⊥AB,FD′⊥CD,EC′⊥CD,
A′,B′,C′,D′为垂足,
则多面体ABCDFE的体积V=VFA′D′-EB′C′+2VF-AA′D′D
=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
5
| ||
| 12 |
点评:本题考查直线与平面垂直的证明,考查多面体的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若a是从集合{1,2,3,4}中随机抽取的一个数,b是从集合{1,2,3}中抽取的一个数,则关于x的方程x2+2ax+b2=0有实数根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某电商在“双十一”期间用电子支付系统进行商品买卖,全部商品共有n类(n∈N*),分别编号为1,2,…,n,买家共有m名(m∈N*,m<n),分别编号为1,2,…,m.若aij=
1≤i≤m,1≤j≤n,则同时购买第1类和第2类商品的人数是( )
|
| A、a11+a12+…+a1m+a21+a22+…+a2m |
| B、a11+a21+…+am1+a12+a22+…+am2 |
| C、a11a12+a21a22+…+am1am2 |
| D、a11a21+a12a22+…+a1ma2m |
方程f(x)=x的根称为f(x)的不动点,若函数f(x)=
有唯一不动点,且x1=1000,xn+1=
(n∈N*),则x2013=( )
| x |
| a(x+2) |
| 1 | ||
f(
|
| A、2006 | B、2008 |
| C、2012 | D、2013 |
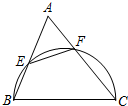 如图,在△ABC中,以BC为直径的半圆分别交AB,AC于点E,F,且AC=2AE,那么
如图,在△ABC中,以BC为直径的半圆分别交AB,AC于点E,F,且AC=2AE,那么