题目内容
在极坐标系中,点(3,
)到直线ρsin(θ-
)=2
的距离为 .
| π |
| 2 |
| π |
| 4 |
| 2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:点P(3,
)化为P(0,3).直线ρsin(θ-
)=2
展开为
(ρsinθ-ρcosθ)=2
,化为x-y=4,利用点到直线的距离公式即可得出.
| π |
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| 2 |
解答:
解:点P(3,
)化为P(0,3).
直线ρsin(θ-
)=2
展开为
(ρsinθ-ρcosθ)=2
,化为x-y=4,
∴点P到直线的距离d=
=
,
故答案为:
.
| π |
| 2 |
直线ρsin(θ-
| π |
| 4 |
| 2 |
| ||
| 2 |
| 2 |
∴点P到直线的距离d=
| |0-3-4| | ||
|
7
| ||
| 2 |
故答案为:
7
| ||
| 2 |
点评:本题考查了极坐标方程化为直角坐标方程、点到直线的距离公式,属于基础题.

练习册系列答案
相关题目
方程f(x)=x的根称为f(x)的不动点,若函数f(x)=
有唯一不动点,且x1=1000,xn+1=
(n∈N*),则x2013=( )
| x |
| a(x+2) |
| 1 | ||
f(
|
| A、2006 | B、2008 |
| C、2012 | D、2013 |
有一个几何体的三视图及其尺寸如图所示,则该几何体的表面积和体积分别为( ) 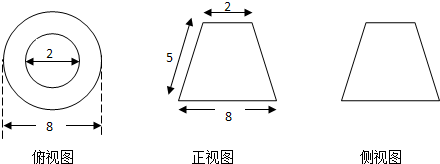

| A、42π,28π |
| B、28π,42π |
| C、24π,28π |
| D、82π,24π |
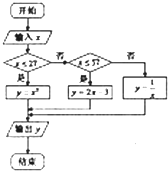 若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,那么函数f(x)-4在x∈R上的零点个数为( )
若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,那么函数f(x)-4在x∈R上的零点个数为( )