题目内容
已知函数f(x)=
则函数y=f(x)-log2x的零点的个数是( )
|
| A、1 | B、2 | C、3 | D、4 |
考点:函数零点的判定定理
专题:计算题,作图题,函数的性质及应用
分析:由题意,函数y=f(x)-log2x的零点的个数即函数f(x)=
与函数y=log2x的交点的个数,作图求解.
|
解答:
解:函数y=f(x)-log2x的零点的个数即
函数f(x)=
与函数y=log2x的交点的个数,
作函数f(x)=
与函数y=log2x的图象如下,

有且仅有两个交点,
故选B.
函数f(x)=
|
作函数f(x)=
|

有且仅有两个交点,
故选B.
点评:本题考查了函数的零点与函数的图象的关系应用,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
某电商在“双十一”期间用电子支付系统进行商品买卖,全部商品共有n类(n∈N*),分别编号为1,2,…,n,买家共有m名(m∈N*,m<n),分别编号为1,2,…,m.若aij=
1≤i≤m,1≤j≤n,则同时购买第1类和第2类商品的人数是( )
|
| A、a11+a12+…+a1m+a21+a22+…+a2m |
| B、a11+a21+…+am1+a12+a22+…+am2 |
| C、a11a12+a21a22+…+am1am2 |
| D、a11a21+a12a22+…+a1ma2m |
方程f(x)=x的根称为f(x)的不动点,若函数f(x)=
有唯一不动点,且x1=1000,xn+1=
(n∈N*),则x2013=( )
| x |
| a(x+2) |
| 1 | ||
f(
|
| A、2006 | B、2008 |
| C、2012 | D、2013 |
下列命题中真命题的个数有( )
(1)集合{小于1的正有理数}是一个有限集;
(2)集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合;
(3)1,
,
,|-
|,0.5,这些数组成的集合有5个元素;
(4)集合{(x,y)|xy≤0,x,y∈R}是指第二和第四象限内的点集.
(1)集合{小于1的正有理数}是一个有限集;
(2)集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合;
(3)1,
| 3 |
| 2 |
| 6 |
| 4 |
| 1 |
| 2 |
(4)集合{(x,y)|xy≤0,x,y∈R}是指第二和第四象限内的点集.
| A、0个 | B、1个 | C、2个 | D、3个 |
定义在R上的函数f(x)满足f(1)=l,且对一切x∈R都有f′(x)<4,则不等式f(x)>4x-3的解集为( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
已知集合M={x|x≥0},P={0,1,2},则有( )
| A、M?P | B、M⊆P |
| C、M∩P=M | D、M∩P=∅ |
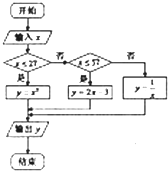 若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,那么函数f(x)-4在x∈R上的零点个数为( )
若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,那么函数f(x)-4在x∈R上的零点个数为( )