题目内容
已知函数f(x)=
与g(x)=mx+1-m的图象相交于A、B两点,若动点P满足|
+
|=2,则P的轨迹方程是 .
| x-2 |
| x+1 |
| PA |
| PB |
考点:轨迹方程
专题:平面向量及应用,直线与圆
分析:联立直线方程和双曲线方程,求得A,B的坐标,写出向量
,
的坐标,求出两向量的坐标和,由向量的模等于2化简整理得到P的轨迹方程.
| PA |
| PB |
解答:
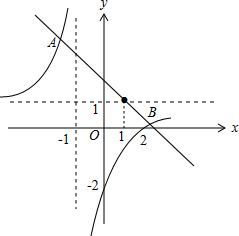 解:如图,
解:如图,
联立
,得mx2=m-3.
∴m>3,x=±
.
当x=-
时,y=-
+1-m,A(-
,-
+1-m).
当x=
时,y=
+1-m,B(
,
+1-m).
设动点P(x,y),
则
=(-
-x,-
+1-m-y),
=(
-x,
+1-m-y).
则
+
=(-2x,2-2m-2y),
由|
+
|=2,得
=2.
两边平方得:4x2+4(y+m-1)2=4,即x2+(y+m-1)2=1(m>3).
∴P的轨迹方程是x2+(y+m-1)2=1(m>3).
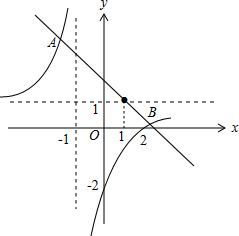 解:如图,
解:如图,联立
|
∴m>3,x=±
|
当x=-
|
| m(m-3) |
|
| m(m-3) |
当x=
|
| m(m-3) |
|
| m(m-3) |
设动点P(x,y),
则
| PA |
|
| m(m-3) |
| PB |
|
| m(m-3) |
则
| PA |
| PB |
由|
| PA |
| PB |
| (-2x)2+(2-2m-2y)2 |
两边平方得:4x2+4(y+m-1)2=4,即x2+(y+m-1)2=1(m>3).
∴P的轨迹方程是x2+(y+m-1)2=1(m>3).
点评:本题考查了轨迹方程的求法,考查了平面向量的坐标运算,是中档题.

练习册系列答案
相关题目
若双曲线C:
-
=1(a>0,b>0)的离心率e∈[
,
],则双曲线C的两条渐近线夹角的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| 2 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
 如图1是一个几何体的主视图和左视图(上面是边长为4的正三角形,下面是矩形),图2是内切于边长为4的正方形),则该几何体的体积为
如图1是一个几何体的主视图和左视图(上面是边长为4的正三角形,下面是矩形),图2是内切于边长为4的正方形),则该几何体的体积为