题目内容
设复数z=1+2i(i为虚数单位),则z2-
等于( )
| 5 |
| z |
| A、4+6i | ||||
| B、-4+6i | ||||
C、
| ||||
| D、-4+2i |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则即可得出.
解答:
解:∵复数z=1+2i(i为虚数单位),
∴z2-
=(1+2i)2-
=-3+4i-
=-3+4i-(1-2i)=-4+6i.
故选:B.
∴z2-
| 5 |
| z |
| 5 |
| 1+2i |
| 5(1-2i) |
| (1+2i)(1-2i) |
故选:B.
点评:本题考查了复数的运算法则,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知角θ的顶点坐标原点,始边与x轴正半轴重合,终边在直线3x-y=0上,则
=( )
sin(
| ||
sin(
|
A、-
| ||||
B、0或
| ||||
C、
| ||||
D、
|
已知集合A={x|x=2k+1,k∈Z},B={x|
≥0},则A∩B=( )
| 1+x |
| 3-x |
| A、[-1,3] |
| B、{-1,1,3} |
| C、[-1,1] |
| D、{-1,1} |
集合A={x|
≥2,x∈Z}的子集个数为( )
| x-1 |
| x+1 |
| A、2 | B、3 | C、4 | D、5 |
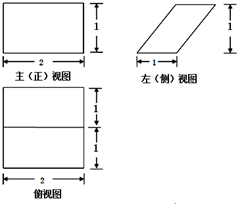
某几何体的三视图如图所示,那么该几何体的表面积为( )

| A、2 | ||
| B、14 | ||
C、6+4
| ||
D、4+6
|